 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Gennaio 2000
Il testo del problema:
Il tetrapak è un contenitore a forma di piramide
triangolare usato tempo fa per alimenti quali il latte al cacao, la panna…
I tetrapak vengono costruiti a partire da un rettangolo:
a) come deve essere piegato un rettangolo per ottenere da esso un tale contenitore?
b) quale relazione deve intercorrere fra le dimensioni del rettangolo affinché il tetrapak sia un tetraedro regolare?
c) è possibile inscrivere un tetraedro regolare in un cubo? come?
Motivare le risposte.
COMMENTO
Abbiamo ricevuto quindici risposte provenienti da tredici scuole di cui tre scuole medie inferiori. Tutte le risposte sono state inviate in "attachment" creando, come abbiamo già segnalato, alcuni problemi tecnici a noi, che le abbiamo ricevute. Ben quattro file Word contenevano un virus: invitiamo quindi le scuole ed i solutori a controllare i computer utilizzati.
Il problema chiedeva prima di descrivere come ottenere un "tetrapak" piegando un rettangolo, poi di determinare le condizioni affinché il poliedro risultasse regolare ed infine come inscrivere quest'ultimo in un cubo.
Fra le quindici soluzioni pervenute:
- una non e' accettabile perché errata nella parte (a) e quindi anche (b);
- un'altra, anche se non errata, presenta una costruzione troppo complessa;
- quattro sono invece errate o carenti nella parte (c).
Nelle altre si riscontrano alcune imprecisioni e/o incompletezze:
- in alcune è stata unificata la parte (a) con la (b) (un tetraedro non è
necessariamente regolare o retto);
- in molte è stata omessa la descrizione della soluzione proposta, facendo
riferimento alla figura (ripetiamo che in questo modo la risposta non si può
presentare via e-mail);
- in alcune non è stata valutata correttamente la relazione del punto (b);
- alcuni hanno scritto il testo nel file della figura (ciò lo rende illeggibile
a coloro che non dispongono dello stesso software).
Le soluzioni proposte per il primo quesito sono sostanzialmente di due tipi, che portano poi a due diversi risultati nel caso (b). Nel terzo quesito quasi tutte le soluzioni presentano la stessa figura (un tetraedro che ha i vertici coincidenti con quattro degli otto vertici del cubo e gli spigoli coincidenti con sei diagonali delle facce del cubo: uno su ciascuna faccia del cubo), non sempre descritta oppure descritta in modo non esauriente.
Le scuole che hanno partecipato sono:
Abbiamo scelto di riportare la soluzione dell'Istituto "Cesaris" di Casalpusterlengo per la sua completezza in quanto presenta entrambi i tipi di soluzione dei punti (a) e (b), anche se necessita di una correzione nella seconda parte. Presentiamo inoltre una delle due soluzioni inviate dall'Istituto "Berenini" di Fidenza, perché si discosta dalle altre. Poiché nessuna delle soluzioni rimaste è completamente soddisfacente, abbiamo scelto, di riportare qui di seguito, un collage di parti di quelle più interessanti.
NOTA: le correzioni o i commenti al testo sono riportate in parentesi quadra.
Soluzione proposta da Alessandra DI FEDE
Classe 2LB Liceo Scientifico Tecnologico "A. Cesaris"
Casalpusterlengo (LO)
|
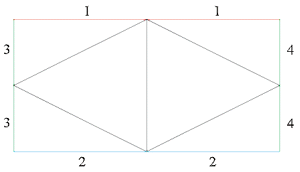
a) Sono possibili due soluzioni, ottenute dai disegni a lato, piegando gli spigoli di colore nero verso l'interno, e facendo combaciare i lati esterni dello stesso colore, identificati in figura con lo stesso numero. |
|
|
b) Affinché il Tetrapak sia un tetraedro regolare, necessita che
il triangolo [che forma ciascuna faccia] sia equilatero.
Da ciò si deduce che, posto il lato del triangolo l=1,
|
|
|
b1) Le relazioni finali che intercorrono fra le dimensioni dei
rettangoli affinché il tetrapak sia un tetraedro [regolare] sono:
Soluzione1: |
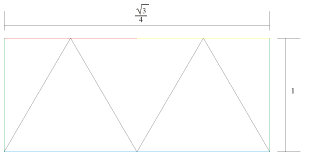 |
Soluzione 2: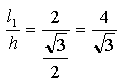
[Nota: i numeri riportati sulla figura non sono quelli utilizzati per calcolare il rapporto, inoltre quello riportato in orizzontale è errato: il valore corretto è 4/(radice di 3)]. |
|
|
c) è possibile inscrivere un tetraedro regolare in un cubo facendo coincidere i 4 vertici del tetraedro con 4 degli 8 vertici del cubo, come nella figura a fianco, di conseguenza i 6 spigoli del tetraedro appartengono ai piani delle facce del cubo, in direzione delle diagonali delle stesse. |
Soluzione proposta da studenti delle classi 1°A e 1°B
Liceo Scientifico Tecnologico dell' ITIS "Berenini" di Fidenza
(PR).
RISPOSTA a)
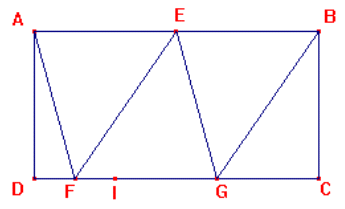
Dato un rettangolo ABCD si considerino i punti E , F, G e I in modo che : i
segmenti AE=EB=FG=1/2 del lato AB, DF+GC=FG, DF=FI (vedi figura nel file
allegato). Per ricavare da questa figura un tetraedro si deve piegare lungo i
segmenti EF ed EG facendo combaciare AE con EB e lungo AF e GB facendo così
unire i lati AD con BC in modo che i punti C e D coincidano entrambi con il
punto I.
RISPOSTA b)
Affinché il tetrapak sia un tetraedro regolare occorre che le sue facce siano
triangoli equilateri. Quindi , poiché il triangolo equilatero , faccia del
tetraedro, ha lato AB/2, la sua altezza deve essere sqrt(3)/4 volte AB e tale
altezza è anche altezza del rettangolo. Quindi AD=(sqrt (3)/4)AB. Inoltre
occorre che I sia punto medio di DC e di conseguenza risulta DF=FI=IG=GC=(1/4)DC.
RISPOSTA c)
Sì, il tetraedro regolare può essere inscritto in un cubo facendo appoggiare i
sei spigoli del tetraedro sulle sei facce del cubo in coincidenza delle
diagonali. Il cubo deve avere quindi lato uguale a sqrt(2)/2 volte lo spigolo
del tetraedro che a sua volta è metà della base AB del rettangolo di partenza.
[lato cubo = (sqrt(2)/4)AB]
============= PARTI DI ALTRE SOLUZIONI (PRIMO METODO) ==============
Parte della soluzione proposta da GRUPPO DI STUDENTI
Seconde Classi Liceo Scientifico "G.GALILEI" di BITONTO
a) [La risposta e' accompagnata da una figura in cui e' riportato un
rettangolo ABCD di altezza AB e base BC.]
Dato un qualsiasi cartoncino rettangolare, per ottenere un tetrapak, lo si deve
piegare a metà due volte lungo la stessa dimensione [per es. lungo la base BC]
e poi una terza volta lungo la [una] diagonale dell'ultimo rettangolo ottenuto.
Spiegando [riaprendo e stendendo] poi il cartoncino si ottiene il rettangolo
ABCD in figura, dove:
- G e' il punto medio di BC,
- M il punto medio di AD,
- F il punto medio di AM,
- E il punto medio di MD.
Le pieghe sono i segmenti FB, FG, EG, EC.
Piegando il rettangolo in maniera che:
- B coincida con C,
- D coincida con A e con M,
si ottiene il tetrapak.
Parte della soluzione proposta dalla classe Terza A
Scuola Media Statale "M. POLO" di ROLO (RE)
b) Il solido che si ottiene è un tetraedro regolare se la base del
rettangolo è il doppio dello spigolo del tetraedro che si desidera ottenere e
l'altezza del rettangolo corrisponde all'altezza di una faccia del tetraedro,
cioè:
AB = 2l; BC = l/2sqrt(3) con l = spigolo del tetraedro [Nella figura AB è la
base e BC e' l'altezza del rettangolo.]
c) sì, è possibile inscrivere un tetraedro regolare in un cubo, basta
tracciare una diagonale in ogni faccia di un cubo come indicato nella figura
n°2, le sei diagonali corrispondono ai 6 spigoli del tetraedro.
============ PARTI DI ALTRE SOLUZIONI (SECONDO METODO) ==============
Parte della soluzione proposta da Michele MEDIOLI
Prima A - Liceo Scientifico Tecnologico dell' ITIS "BERENINI" di
FIDENZA (PR).
RISPOSTA a)
Dato un rettangolo ABCD si consideri il rombo inscritto EHFG [Le lettere sono in
senso orario, il punto E su AB]
Per ricavare da questa figura un tetraedro si deve piegare lungo i segmenti EF
ed EG, GF, FH, HE, facendo combaciare AE con EB, AG con GD, DF con FC e CH con
HB, e facendo così combaciare i quattro vertici del rettangolo.
RISPOSTA b)
Affinché il tetrapak sia un tetraedro regolare occorre che le sue facce siano
triangoli equilateri.
Per fare in modo che ciò avvenga, il lato AD deve essere uguale al lato GE
(mezza diagonale del rettangolo = BD/2) e AB, quindi, deve essere uguale a sqrt(BD^2-AD^2),
ma essendo BD = 2AD, la formula verrà semplificata in sqrt((2AD)^2-AD^2) = sqrt(4AD2-AD2)
= sqrt(3AD^2) = = ADsqrt(3).
| Home Page Cabri | Torna a FLATlandia | Archivi |