 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandia
"Abbi pazienza, ché il mondo vasto e
largo". (Edwin A. Abbott)
Febbraio 2000
Il testo del problema:
In un triangolo ABC siano D, E e F, i punti medi rispettivamente dei lati AB, BC e AC.
a) Quale è il legame che intercorre fra la
superficie del quadrilatero BEFD e quella dei triangoli AEF e FCD?
b) Cosa accade se il punto F è un punto qualunque del lato AC?
Giustificare le risposte.
COMMENTO
Il problema proponeva due quesiti di cui il primo, molto
semplice per non scoraggiare gli allievi più giovani, era un caso particolare
del secondo.
Abbiamo ricevuto diciannove risposte provenienti da diciassette scuole di cui
due di Scuola Media Inferiore.
Le scuole che hanno partecipato sono:
Tutti hanno risolto, più o meno correttamente, il primo
quesito, ma solo alcuni hanno risposto al secondo o lo hanno fatto in modo
incompleto o addirittura errato.
In un messaggio precedente vi abbiamo invitato a giustificare le vostre
affermazioni indicando le proprietà utilizzate anche se abbastanza note (come
quella dei punti medi che ricorre nelle dimostrazioni dei due quesiti).
Questa volta vi invitiamo ad essere più concisi: basta che le giustificazioni
siano chiare ed esaurienti e quindi non è necessario eccedere nei passaggi o in
dettagli.
Dobbiamo inoltre invitarvi ancora ad un uso corretto dei
simboli matematici:
- alcuni hanno usato il simbolo "=" per esprimere sia la congruenza di
figure sia per indicarne l'equivalenza;
- ricordiamo che con le scritture "ABC", "ABCD", in genere
si indicano figure non la loro area.
Riportiamo qui di seguito, per la loro semplicità e chiarezza, anche se necessitano di qualche correzione formale, le soluzioni (complete) degli allievi della SM "L. Valenziano", simile nella seconda parte alla soluzione inviata da due allieve dell'ITI "Berenini", e quella del LS "G.Galilei" di Catania.
Di seguito troverete anche la soluzione (completa) del LS "G. Ferraris", la risposta al secondo quesito del LS "G. Galilei" di Bitonto, e quella al primo della SM "Bellotti".
NOTA: le correzioni o i commenti al testo sono riportate in parentesi quadra.
Soluzione di De Icco Roberto e Merli
Marco della classe III D (t.p.)
Scuola Media St. "Luca Valenziano" di Tortona (AL)
1) Area(BEFD) = Area(AEF) + Area(FCD)
GIUSTIFICAZIONE
Il triangolo BED è metà del parallelogrammo BEFD
[l'affermazione che BEFD è un parallelogrammo non è motivata]; l'altra metà
è il triangolo DEF.
DEF è però anche la metà di altri due parallelogrammi DECF e DEFA.
Allora i triangoli AEF e FCD, metà rispettivamente dei parallelogrammi DEFA e
DECF sono equiestesi ed entrambi la metà del parallelogrammo BEFD.
2) Se F1 e' un punto qualsiasi di AC vale ancora la relazione Area(BEF1D) = Area(AEF1) + Area(F1CD)
GIUSTIFICAZIONE
Se F1 e' un punto qualsiasi di AC i triangoli CF1D e AF1E
sono, rispetto a CFD e AFE, uno aumentato e l'altro diminuito di due superfici
equivalenti (F1FD e F1FD).
Quindi la somma delle due aree è invariata.
Anche i triangoli F1ED e FED hanno la stessa area perché hanno stessa base (DE)
e stessa altezza poiché AC è parallelo a DE.
Quindi vale la relazione.
Soluzione proposta da Daniele Urzì
della IIa B
Liceo Scientifico St. "G.Galilei" di Catania
(figure in Cabri realizzate da Carlo
Longhitano della stessa classe)
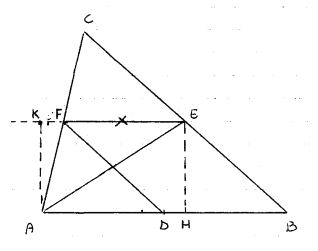
In riferimento alla figura 1 (del file FIG1E2.FIG),
premettiamo che i segmenti FE, DF, DE, poiché congiungono i punti medi dei lati
del triangolo ABC sono rispettivamente paralleli ad AB, BC, CA e rispettivamente
uguali [CONGRUENTI] alla metà di questi.
Da questa premessa deduciamo che il quadrilatero DBEF è un parallelogrammo.
Su di esso la trasversale [DIAGONALE] DE individua i due triangoli uguali
[CONGRUENTI] DEF e DBE.
I triangoli AEF, CFD e FDE sono equivalenti perché hanno uguali [CONGRUENTI] le
basi AF, FC, DE e le altezze ad esse relative uguali (tali altezze sono uguali
[CONGRUENTI] alla distanza fra i segmenti paralleli
AC e DE). Ciò significa che la superficie di ciascuno dei triangoli AEF e FDC
è equivalente alla metà della
superficie del parallelogrammo DBEF.
Consideriamo il caso in cui il punto F sia un punto
qualunque di AC (figura 2 del file FIG1E2.FIG ).
I triangoli FDC e FCE sono equivalenti perché hanno la base FC in comune e le
altezze ad essa relativa uguali [CONGRUENTI] (sono le distanze fra i segmenti
paralleli AC e DE, condotte dai punti D e E).
Questo significa che la somma delle superfici dei triangoli AEF e FDC e'
equivalente alla superficie
del triangolo ACE.
In maniera analoga a quanto fatto in precedenza si dimostra l'equivalenza dei
triangoli ADE e FDE, da cui deriva l'equivalenza delle superfici del
quadrilatero DBEF e del triangolo ABE.
Quest'ultimo è equivalente al triangolo ACE (infatti hanno le basi CE ed EB
uguali e l'altezza AH ad esse relativa in comune): così e' dimostrato che, se F
è un punto qualunque di AC, la somma delle superfici dei triangoli AEF e CFD e'
equivalente alla superficie del quadrilatero DBEF.
Soluzione proposta da Raffaello Moroni,
Cl. II°E
Istituto Tecnico Industriale "Galileo Ferraris", S. Giovanni
Valdarno (Ar)
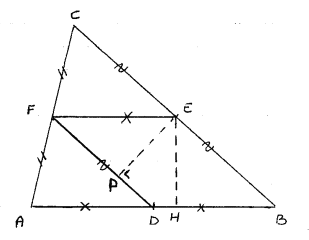
Parte a)
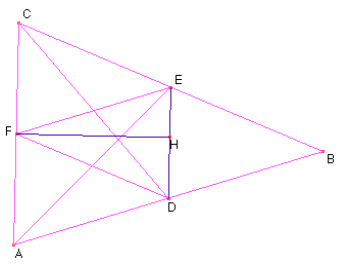
Il segmento DE è parallelo ad AC e congruente ad AF e CF
in quanto, in un qualsiasi triangolo, il segmento congiungente i punti medi di
due lati è parallelo al terzo e congruente alla sua metà.
Il segmento FH, perpendicolare a DE è altezza del triangolo DEF rispetto alla
base DE. Ma è anche congruente all'altezza di AEF rispetto ad AF in quanto DE
è parallelo ad AC. I triangoli DEF e AEF sono quindi equivalenti in quanto
hanno la stessa altezza e la stessa base.
Il quadrilatero BEFD è un parallelogramma, in quanto EF è parallelo ad AB (E
ed F punti medi) e DE è parallelo ad AC, e DE è diagonale.
DEF è quindi congruente ad EDB (la diagonale divide un parallelogramma in
triangoli congruenti).
AEF è quindi la metà del quadrilatero. Essendo poi AF = FC ed FH altezza sia
di AEF che di FCD, i due triangoli sono equivalenti.
Quindi la relazione fra le superfici è ![]()
Parte b)
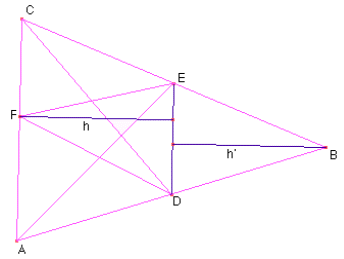
La somma delle aree dei triangoli AEF e FCD è:
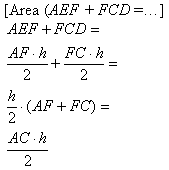
Le altezze h e h' sono congruenti in quanto, considerando la parallela a DE per B, segmenti sulla perpendicolare corrispondenti a segmenti congruenti (CE=BE poiché E è punto medio). L'area del quadrilatero BEFD è data dalla somma delle aree dei triangoli DEF e BED:
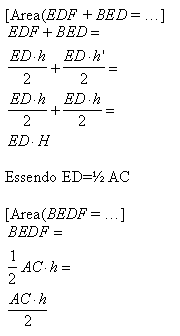
Quindi, se il punto F è un punto qualunque del lato AC la
somma dei triangoli AEF e FCD è equivalente a BEFD.
Soluzione alla parte b) del problema proposta da
Seconde classi Liceo Scientifico "Galileo Galilei" Bitonto (BA)
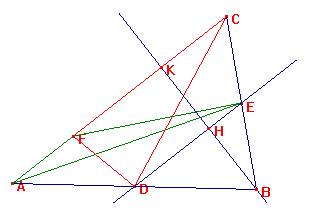
Parte b)
Se F è un punto qualunque di AC si ha che: AFD = AFE
["=" si legga equivalente] avendo stessa base e altezze congruenti in
quanto distanze fra DE // AC; analogamente FCD = FCE [come sopra].
Ne consegue che AFE+FCD = AFD+FCE (1) [come sopra].
Per il teorema di Talete applicato alle rette parallele DE e AC, l'altezza BK
del triangolo ABC relativa ad AC è divisa in parti congruenti da DE per cui FED
= BDE [come sopra], avendo stessa base e altezze congruenti (BH=HK).
DBE = 1/4 ABC ["=" sta per equivalente], avendo DE = 1/2 AC e BH = 1/2
BK, pertanto BEFD = 1/2 ABC [equivalente].
Ne consegue che AFD+FCE = 1/2 ABC [equivalente] e quindi da (1) BEFD = AFE+FCD
[equivalente].
Soluzione proposta da gruppo di alunni
delle classi 3A e 3C
Scuola Media Statale B. Bellotti - Busto A. (VA)
 |
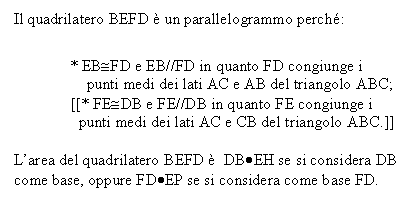 |
 |
 |
 |
 |
Concludendo: l'area del parallelogrammo BEFD è equivalente alla somma delle aree dei due triangoli AEF e FCD.
| Home Page Cabri | Torna a FLATlandia | Archivi |