 FLATlandia
FLATlandia"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)
 FLATlandia
FLATlandiaQuesta pagina contiene animazioni CabriJava.
Selezionare qui per tornare alla pagina con solo immagini
fisse.
Dicembre 1999
Il testo del problema:
Data una circonferenza di centro O e raggio r ed un punto P interno ad essa:
a) costruire la corda di lunghezza minima passante per P;
b) individuare, mediante una costruzione, un punto P in modo che la corda richiesta sia lato di un quadrato inscritto nella circonferenza;
c) determinare in funzione di r la distanza PO dei punti P che soddisfano la condizione (b) e descrivere quale figura formano tali punti.
Ai ragazzi del biennio di scuola secondaria superiore si chiede di giustificare le costruzioni dei precedenti punti (a) e (b).
COMMENTO
(Con animazioni CabriJava)
Abbiamo ricevuto sedici risposte provenienti da quattordici scuole di cui una elementare e quattro medie inferiori.
Il problema richiedeva due costruzioni e la individuazione di un luogo di punti.
La costruzione richiesta nel punto (a) non sempre e' stata giustificata dai ragazzi delle superiori e in alcune risposte non lo e' stato in modo corretto.
In tutte le risposte pervenute la soluzione del punto (b) e' stata affrontata a partire dal risultato finale: costruendo cioe' il lato del quadrato inscritto per individuare il punto P richiesto.
Considerare il problema come risolto è uno dei metodi più fruttuosi già seguito dagli antichi geometri greci, ma dovrebbe condurre poi ad individuare un percorso di risoluzione.
Presentiamo, in fondo a questo commento, una nostra proposta di soluzione.
Le scuole che hanno partecipato sono:
Essendo le risposte accolte molto simili fra loro, ne abbiamo scelte due sole da riportare: quella della scuola media "Bellotti", a cui diamo il benvenuto nel mondo di FLATlandia, e quella del LS "Scorza".
NOTA: Nelle soluzioni riportate, le correzioni o i commenti sono scritti fra parentesi quadre.
Immagini animate CabriJava
|
|
|
Nostra proposta di soluzione punto (b):
Preso un punto Q sulla circonferenza, si costruisce il quadrato avente come diagonale il raggio QO.
Ciascuno degli estremi dell'altra diagonale e' uno dei punti P richiesti.
Soluzione proposta da:
Gruppo di alunni delle classi 3A e 3C
Scuola media statale "B. Bellotti" - Busto Arsizio (VA)
a) Disegno una circonferenza di centro O e individuo un punto P interno ad essa.
Traccio il raggio OC passante per P e disegno la corda AB perpendicolare ad OC.
AB è la corda minima passante per il punto P.
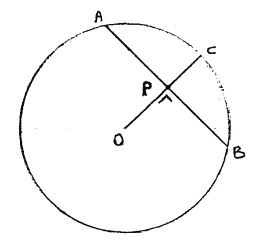
(nota: immagine non animata)
b) Disegno una circonferenza di centro O, traccio un diametro AB e un raggio OC che forma un angolo di 45° con AB.
Traccio la corda CD perpendicolare ad AB: il punto P in cui la corda incontra il raggio OB si trova sulla corda CD che è il lato del quadrato inscritto nella circonferenza.
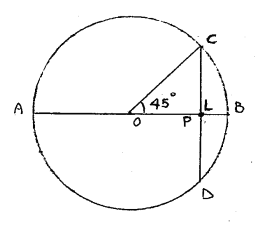
(nota: immagine non animata)
Dimostrazione:
Se POC angolo=45° e OPC angolo=90° per costruzione, allora PCO angolo=45°.
Se supponiamo OC=sqr(2) allora, per il teorema di Pitagora, PC=OC/sqr(2)=1 e di conseguenza CD=2
Siccome un quadrato inscritto il lato è uguale al diametro fratto sqr(2), nel nostro caso il lato del quadrato dovrebbe essere l=2sqr(2)/sqr(2)=2 che è la lunghezza del segmento CD.
c) PO è il cateto del triangolo rettangolo isoscele POC che ha ipotenusa congruente al raggio della circonferenza. Di conseguenza PO=r/sqr(2)
I punti P che soddisfano tale condizione formano una circonferenza concentrica interna a quella di partenza.
Soluzione proposta da:
Ugo Campisani e Giovanna Turco
Classe II Sez.C Liceo Scientifico "Scorza" Cosenza
a)Data una circonferenza di centro O ed un punto P interno ad essa, la corda minima passante per P è quella perpendicolare alla retta che contiene OP. Infatti considerando un’altra corda CD passante per P, tracciamo la distanza di essa dal centro e sia OQ. Il triangolo OPQ è rettangolo in Q (OQ è perpendicolare a CD), l’ipotenusa OP è maggiore di OQ, pertanto la corda AB la cui distanza dal centro è OP sarà minore di CD e di qualunque altra corda.
b) Per individuare il punto P, costruiamo un quadrato inscritto nella circonferenza tracciando due diametri perpendicolari. I punti di intersezione con la circonferenza sono vertici del quadrato. Il punto P sarà il punto medio di ogni lato perché è il punto di intersezione della bisettrice dell’angolo formato dai due diametri con il lato del quadrato.
c)La distanza OP è un cateto del triangolo rettangolo OPB retto in P; l’ipotenusa è il raggio .Sappiamo che per il teorema di Pitagora il quadrato costruito sull’ipotenusa è uguale alla somma dei quadrati costruiti sui cateti. Quindi ,se OP è uguale a PB e siano essi i cateti del triangolo considerato r2=2OP2[leggasi r al quadrato=2*(OP al quadrato)] implica che OP=r/(Radice quadrata di 2).
I punti P sono gli infiniti punti di una circonferenza che ha per centro O e per raggio OP. Infatti, tracciando altri diametri perpendicolari e le bisettrici degli angoli formati da essi, si può ottenere un infinito numero di punti P che si trovano sempre alla stessa distanza da O.
Quindi, sapendo che il raggio è la distanza di un qualsiasi punto della circonferenza dal centro, OP è il raggio della nuova circonferenza ottenuta.
| Home Page Cabri | Torna a FLATlandia | Archivi |