Soluzioni Aprile 2000

FLATlandia
"Abbi pazienza, ché il mondo vasto e largo". (Edwin A. Abbott)

Aprile 2000

Il testo del problema:

E' data una semicirconferenza c di diametro AB, centro O e raggio r.

a) Costruire il quadrato SPQR in essa inscritta, col lato SP sul diametro AB. Giustificare la costruzione.

b) Calcolare in funzione di r il lato del quadrato così inscritto.

COMMENTO

Abbiamo ricevuto quattordici risposte provenienti da dieci scuole di cui due media inferiore. Una delle risposte proveniva da allievi di una scuola secondaria superiore che hanno partecipato per la prima volta. Purtroppo la soluzione da loro proposta non è tra quelle accettate: auguriamo a questi ragazzi di fare meglio con il quesito di maggio.
Anche nel problema di questo mese era richiesta, nella prima parte, una costruzione: si trattava quindi di individuare, e giustificare, una strategia per ottenere la figura proposta. Tre delle risposte pervenute non hanno perseguito questo obiettivo e quindi non sono state accettate.
Tutti invece hanno risposto correttamente alla seconda parte del problema in cui si chiedeva di calcolare una misura.

Le scuole che hanno partecipato sono:

SM di Roveredo in Piano (PN)
SM "G. Pascoli" di Castelbolognese (RA), due risposte
ITI "Berenini" di Fidenza (PR), due risposte
ITI "G. Ferraris" di S. Giovanni Valdarno (AR)
ITI "E. Ferrari" di Torino (TO), tre risposte
ITG "M. Buonarroti" di Caserta (CE)
LS "G. Galilei" di Catania
LS "G. Galilei" di Bitonto (BA)
LS "Pitagora" di Rende (CS)
LS "Patrizi" di Cariati (CS)

Fra le risposte che sono state accolte abbiamo individuato diversi modi per ottenere la costruzione richiesta: riporteremo una soluzione per ciascun tipo (e, per ciascuna soluzione, indicheremo le scuole che hanno inviato risposte analoghe).
Non verranno riportate via e-mail le risposte ( in generale al secondo quesito) di chi ha usato editor particolari in quanto, come abbiamo più volte precisato, non sono adatti ai messaggi e-mail.
Presenteremo inoltre sul sito web (http://arci01.bo.cnr.it/cabri/flatlandia/), per la sua completezza, la soluzione (completa) del LS "G. Galilei" di Bitonto che propone due diverse costruzioni (la prima delle quali è uguale a quella inviata dall'ITG "Buonarroti"), e, per la sua originalità, quella del LS "G. Galilei" di Catania.

Soluzione proposta da:
Seconde classi Liceo Scientifico "Galileo Galilei" Bitonto (BA)

(la prima costruzione è uguale a quella inviata dall'ITG "Buonarroti")

Parte a)
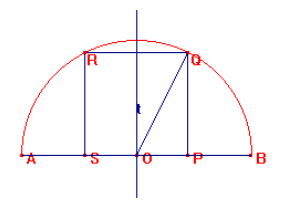
Se SPQR è il quadrato inscritto nella semicirconferenza c di diametro AB, centro O e raggio r, si osserva che il triangolo rettangolo OPQ ha il cateto OP=1/2 PQ, per la simmetria rispetto alla retta t passante per O e perpendicolare ad AB.

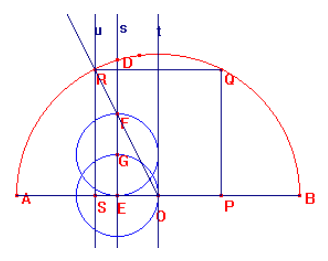
Da questa osservazione nasce l'idea per la seguente costruzione del quadrato inscritto nella semicirconferenza:

tracciamo la semicirconferenza c di diametro AB=2r e centro O;
prendiamo un punto E qualsiasi sul diametro AB;
tracciamo la retta s per E perpendicolare ad AB e stacchiamo su questa un segmento EF=2 EO, mediante una prima circonferenza c' di centro E e raggio EO e una seconda circonferenza c'' di centro G, intersezione tra c' ed s, e raggio EG;
sia R l'intersezione tra la semiretta OF e la semicirconferenza c e tracciamo per R la retta u perpendicolare ad AB nel punto S. Il triangolo SOR è simile ad EOF e pertanto ha SO=1/2SR;
RS è il lato del quadrato inscritto nella semicirconferenza c;
Completiamo la costruzione del quadrato tracciando il punto P simmetrico di S rispetto ad O ed il punto Q simmetrico di R rispetto a t.

Parte a) bis
La costruzione del quadrato inscritto nella semicirconferenza c può essere fatta anche nel seguente modo:

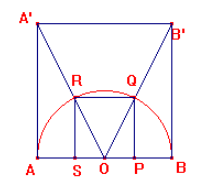
Costruiamo il quadrato ABB'A' di lato AB che contiene la semicirconferenza;
uniamo i vertici A' e B' con il centro O e siano R e Q i punti di intersezione con la circonferenza ;
da R e da Q mandiamo le perpendicolari ad AB che lo intersecano in S e P, ottenendo il quadrilatero SPQR inscritto nella semicirconferenza ;
verifichiamo che SPQR è un quadrato:

i triangoli OPQ e OBB' sono simili avendo l'angolo POQ in comune, gli angoli OPQ = OBB' retti pertanto QP:BB'=OQ:OB'; simmetricamente sono simili i triangoli SOR e AA'O; i triangoli A'B'O e RQO, avendo l'angolo ROQ in comune e i lati che lo comprendono in proporzione, sono simili per il 2° criterio e quindi RQ è parallelo ad A'B' e si ha che RQ:A'B'=OQ: OB'. Per transitività RQ:A'B'=QP:BB'= SR:A'A. SPQR è quindi simile ad ABB'A' e pertanto è esso stesso un quadrato.

Parte b)
Per calcolare il lato l del quadrato inscritto in funzione di r, applichiamo la relazione pitagorica al triangolo SOR:
l ²+ (l/2) ² = r² da cui l ² = 4/5 r² e quindi l = (2 r sqr 5) /5

Soluzione proposta da
Daniele Urzì
Classe IIB Liceo Scientifico Stata Galileo Galilei (Catania)

a) Siano OC il raggio perpendicolare ad AB ed M il suo punto medio (MO MC r/2). Puntando il compasso in M e con apertura uguale ad MO si tracci una circonferenza t. Si unisca A con M e sia D il punto di intersezione del segmento AM con t. Dal punto D si tracci una retta perpendicolare ad AB, che interseca AB in un punto S e la semicirconferenza iniziale in un punto R.
Dal punto R si conduca la perpendicolare ad SR e sia Q il punto di intersezione con la semicirconferenza di partenza; si tracci da Q la perpendicolare a QR e sia P il suo punto d'intersezione con AB. Ricordando che la somma degli angoli interni di un quadrilatero è congruente a due angoli piatti, in riferimento al quadrilatero SPQR, l'angolo SPQ è retto.
Il rettangolo SPQR così ottenuto è il quadrato richiesto. Infatti, dimostriamo algebricamente che due suoi lati consecutivi sono congruenti.
Si dimostra facilmente che CO è l'asse di RQ. Quindi, essendo i segmenti SP ed RQ uguali e paralleli, CO è anche asse di SP (in particolare SO OP ).
Applicando il teorema di Pitagora al triangolo rettangolo AOM si trova :

Si considerino le trasversali AM ed AO alle parallele SR e CO, per la corrispondenza di Talete si ha AM / AO = DM / SO, sostituendo

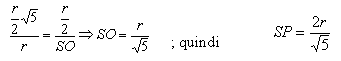
Dal teorema di Pitagora Applicato al triangolo rettangolo SOR si ricava
Quindi essendo RS SP rimane dimostrato che il rettangolo SPQR è il quadrato cercato.

b) Dalla giustificazione da noi trovata si deduce facilmente che il lato l di un quadrato inscritto in una semicirconferenza di raggio r è

NOTA: si può dimostrare che il segmento AD è la parte aurea del raggio r.

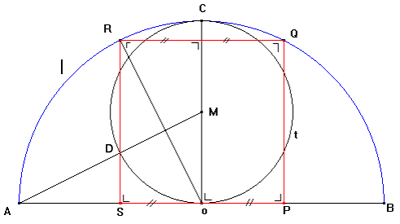
Figura in Cabri II di Carlo Longhitano

Soluzione proposta da
Classe 2^ A
Scuola Media Statale di Rovaredo in Piano (PN)
(è sezione staccata della scuola media “G.Zanella” di Porcia)

[Nota: la figura B e' quella relativa al problema proposto; la figura A mostra la costruzione del segmento MN, citato successivamente, a partire dal triangolo rettangolo isoscele LMT con angolo retto in L]

In un quadrato inscritto in una semicirconferenza il punto medio del lato sul diametro coincide con il centro. Il raggio è l’ipotenusa di un triangolo rettangolo in cui un cateto è doppio dell’altro (s’immagini il triangolo OPQ nella Fig.B). Se consideriamo il cateto minore pari all’unità, l’ipotenusa è sqrt5.
Costruiamo un segmento unitario ed uno pari a sqrt5 da impiegare nella composizione B. Sarebbe sufficiente disegnare un triangolo rettangolo i cui cateti stanno nel rapporto 1 a 2, ma preferiamo proporre la costruzione della Fig. A in quanto rappresenta una procedura generale per ottenere segmenti pari a sqrt2, sqrt3, sqrt4, sqrt5 (MN), ecc., essendo LM ed LT segmenti unitari ed i triangoli considerati tutti rettangoli.

a)
1. Circonferenza c di centro O; retta r passante per O; intersezioni di c ed r (A,B).
2. Semiretta s di origine O; compasso di centro O e raggio LM (Fig. A), intersezione con s: punto C; compasso di centro O e raggio MN (Fig. A), intersezione con s: punto D.
3. Segmento BD; retta t parallela a BD passante per C; intersezione r con t: punto P. (Per il Teorema di Talete i segmenti OP ed OB sono nel rapporto di 1 a sqrt5).
4. Retta u per P, perpendicolare ad r, e sua intersezione con c: Q, Q’; retta v per Q, parallela ad r, e intersezione con c: punto R; retta z per R e perpendicolare ad r, intersezione tra le due rette: punto S. Poligono (quadrato) PQRS.

b)
Il raggio della semicirconferenza misura sqrt5 quando il lato del quadrato è di 2, quindi il lato è pari al doppio del rapporto tra il raggio e sqrt 5.

Soluzione (prima parte) proposta da
Michele Medioli
Classe I-A del liceo Scientifico Tecnologico dell'ITI "Berenini"
(analoga risposta hanno inviato gli allievi del LS "Pitagora").

Risposta A)

COSTRUZIONE
Data la semicirconferenza AB di centro O, costruire il quadrato ABCD sul diametro AB ed unire i vertici C e D con il punto O. I segmenti CO e DO intersecano la semicirconferenza nei punti Q e R . Siano S e P le proiezioni ortogonali di R e Q sul diametro AB . Si dimostra che SPQR è il quadrato richiesto:

DIMOSTRAZIONE
I triangoli AOD e BCO sono congruenti perché sono triangoli rettangoli con i cateti congruenti.
I triangoli SOR e AOD sono simili, perché sono rettangoli e hanno un angolo in comune; analogamente per i triangoli PQO e BCO.
Inoltre i triangoli SOR e PQO sono congruenti per essere simili a figure congruenti e per avere RO congruente a QO.
Essendo DA il doppio di AO, anche RS è doppio di SO e QP è il doppio di PO:
dunque si ha RS congruente a SP che è congruente a PQ.
La figura SPQR è un quadrato avendo 3 lati congruenti e i due angoli compresi retti.

Soluzione (prima parte) proposta da
Alberto Boscaggin e Paolo Gurgo
Classe II-A s.t. dell'ITI "E. Ferrari"
(analoga risposta hanno inviato gli altri allievi dello stesso istituto
e quelli degli ITI "Berenini"(I-B) e "G. Ferraris")

A) Costruiamo un triangolo OBH, rettangolo in B e avente OB per cateto minore e BH = 2r per cateto maggiore.
Indichiamo con Q il punto di intersezione tra il segmento OH e la semicirconferenza e con P la proiezione di Q su diametro AB.
Individuiamo i punti S e R, simmetrici di P e Q rispetto all'asse del segmento AB. Il quadrilatero SPQR è un quadrato.

Giustificazione:
Il triangolo OPQ è simile al triangolo OBH poiché hanno un angolo in comune HOB e un angolo retto.
Quindi possiamo scrivere, HB : PQ = OB : OP cioè, 2r : l = r : OP da cui OP = l/2
Poiché SO = OP , SP = PQ = l
Poiché la costruzione è simmetrica rispetto all'asse del segmento AB, il triangolo OSR è congruente al triangolo OPQ. Quindi il quadrilatero SPQR è un quadrato.

| Home Page Cabri | Torna a FLATlandia | Archivi |