FLATlandia

Ottobre 1998

Il problema:

Dati i segmenti

M +---+---+---+---+---+ N

P +---+---+---+---+---+---+ Q

R +---+---+---+---+ T

costruire un triangolo ABC in modo che:

1. AB = MN;
2. l'altezza relativa al lato AB misuri come RT;
3. la mediana relativa al lato BC misuri come PQ.

1. Motivare la costruzione.
2. Esiste un'unica soluzione?
3. Esplorare le possibilità di soluzione per una qualunque scelta dei tre segmenti.
   

N.B.: L'unità di misura, O +---+ U, può essere fissata a piacere.

Soluzioni:

Nota:  per modificare la figura muovere i punti N, Q, T

Sono giunte in tutto otto risposte provenienti da sei scuole, di cui una sola è una scuola media inferiore.
Il problema richiedeva una costruzione, la sua motivazione e l'analisi della sua generalizzazione.
Una risposta contiene solo un cabri-disegno senza alcuna descrizione e quindi non è accettabile.
Nessuna delle rimanenti risposte ha affrontato in modo esauriente tutti i quesiti posti: la più completa, e anche la più corretta come esposizione, è quella proveniente dal Liceo Scientifico "Galilei" di Adria.
Nessuno ha rilevato che la generalizzazione del problema è possibile solo quando i segmenti PQ ed RT assegnati sono tali che PQ > 2RT.
Oltre a varie pecche di linguaggio, abbiamo rilevato alcune imprecisioni concettuali che qui elenchiamo:

• non tutti hanno rispettato le lunghezze assegnate;
• una retta ed una circonferenza in genere hanno due punti di intersezione, quindi si dovevano individuare almeno due soluzioni nello stesso semipiano!
• se con le lettere minuscole si indicano le rette, non si può parlare del "punto medio di p"!
• il problema richiedeva una costruzione e non sempre è stato precisato come ottenere la distanza di un punto da una retta o fra due rette (eppure basta mandare una perpendicolare), o come riportare una distanza fra due punti (anzichè usare il righello, che è uno strumento poco preciso, basta tracciare, come facevo già i Greci, una circonferenza);
• chi ha provato a dare una motivazione non lo ha fatto in modo esauriente o non ha citato il teorema utilizzato (bastava menzionare il fascio di rette parallele tagliato da trasversali o il suo corollario).

Siamo convinti che farete tesoro di quanto qui rilevato e che prima di rispondere ai prossimi quesiti metterete un pò più attenzione nel leggere il testo del problema e nell'esporre la soluzione. In ogni caso l'importante è partecipare: è un modo per accrescere e migliorare tutti insieme le nostre conoscenze.

Sono pervenute risposte dalle seguenti scuole:

• SM "Testoni-Fioravanti", Bologna
• ITG "Rondani", Parma
• ITI "Cesaris", Casalpusterlengo (LO)
• ITI "Euganeo", Este (PD)
• LS "Galilei", Adria (RO)
• LS "Mascheroni", Bergamo

Riportiamo due risposte ai quesiti a) e b).

NOTA: Nelle soluzioni abbiamo messo tra parentesi quadre le correzioni o i commenti al testo.

------------------------------

Studente:Pignoletti Alberto
Classe: 1Bst
Istituto: ITIS "Euganeo" - ESTE (PD)

Proposta di Soluzione del Problema del Mese:

Sapendo che il segmento di base AB corrisponde al segmento MN, che misura secondo le mie indicazioni 5 cm, lo traccio e agli estremi scrivo le lettere A e B.

Traccio la retta (c) parallela al segmento AB alla distanza di 4 cm [come si ottiene?] (che conterrà il punto C), che può essere sia sopra che sotto al segmento AB (quindi se trovo un triangolo esisterà anche il simmetrico rispetto alla retta AB.
Traccio la retta intermedia (m) [parallela a c, passante per il punto medio  della distanza] tra il segmento AB e la retta tracciata in precedenza per trovare la retta che conterrà il punto M dove cadrà la mediana.
Punto il compasso nel punto A e traccio una circonferenza di raggio 6 cm che interseca la retta intermedia (m) nel punto M e nel punto M'.
Congiungo il punto B con il punto M e B con M' e prolungo ciascunodei due segmenti fino alla retta (c) parallela al segmento AB.
Fatto ciò congiungo il punto A con il punto C [e C'].
La soluzione non è unica, esiste anche il triangolo simmetrico di ciascuno di questi rispetto all'asse AB. I triangoli sono quindi 4.

-------------------------------------------------

Studenti: Piazzon Mauro, Rocchi Matteo, Santarato Enrico e Sartori Paolo
Classe: 2° A-PNI
Istituto: Liceo Scientifico Statale "Galileo Galilei" - ADRIA (Rovigo)

a)

Stabilita un'unità di misura u.

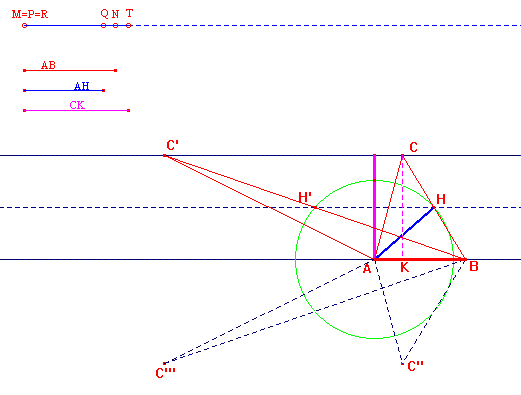
Su una retta r si prende il segmento AB misurante 5u. Si tracciano le rette s e t parallele ad AB, situate su semipiani opposti di bordo AB e distanti da AB 4u [come si tracciano?]; e le rette m e n sempre situate su semipiani opposti di bordo AB, distanti 2u da AB e parallele ad AB.

Tracciare la circonferenza di centro A e di raggio 6u, che interseca le rette m e n nei punti M e M', su m, e M'', M''', su n; questi punti saranno i punti medi dei segmenti BC, BC', BC'' e BC''', passanti rispettivamente per M, M', M'' e M''', e aventi C e C', appartenenti a s, e C'' e C''', appartenenti a t. Infatti la retta m taglia a metà qualunque segmento che ha un estremo in B e un altro in un punto C di s, e CM = MB; quindi l'estremo M nella mediana AM, relativa a BC, deve cadere sulla retta m. Analogamente succederà per la retta n.
Pertanto congiungendo A con i punti M, M', M'' e M''', si troveranno le mediane dei quattro triangoli scaleni ABC, ABC', ABC'' e ABC''', ognuno di altezza 4u.

b)

Non esiste una sola soluzione, ma ben quattro, come visto nel punto a).

Arrivederci a Novembre con il prossimo problema!

Giuliana BETTINI

Franca NOE'

Consolato PELLEGRINO

 

| Il problema | Come partecipare | | Archivi | Calendario | | Scuole | | Altri problemi |