 FLATlandia
FLATlandia FLATlandia
FLATlandia
Novembre 1998
Il problema:
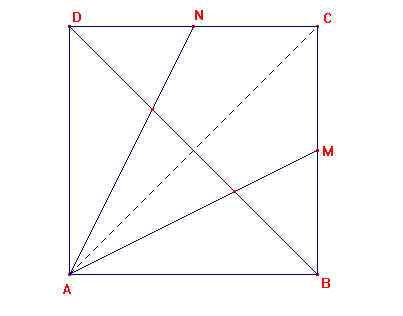
Dato un quadrato ABCD, dal vertice A escono due segmenti che lo
congiungono con i punti medi M e N rispettivamente dei lati BC e CD.
Questi segmenti dividono una diagonale del quadrato in tre parti congruenti.
a) Riesci a motivare questa asserzione?
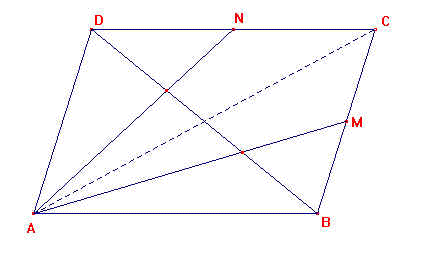
b) Questa proprietà vale anche in altri quadrilateri? Quali? Perché?
Soluzioni:
Abbiamo ricevuto in tutto nove risposte provenienti da otto scuole di cui quattro scuole medie inferiori.Tre sono le risposte complete e corrette (a parte alcune imprecisioni nella esposizione), nelle quali e' stata individuata la proprieta' generale che permette di rispondere sia alla domanda a), sia alla domanda b).
Le scuole che hanno partecipato sono:
In questa occasione si sono distinti particolarmente i ragazzi della scuola media e per questo abbiamo scelto di presentare due loro risposte: una completa, dell'altra solo la prima parte.
NOTA: Le correzioni al testo sono fra parentesi quadre. Le parti superflue sono fra doppie parentesi quadre.
-----------------------------------------------------
Soluzione della classe 3°A della scuola media "Carlo Jussi" di San Lazzaro di Savena - Bologna
(Questa soluzione e' simile a quelle inviate da Murgia Salvatore e Contu Ivan di Cagliari e da Curotti Alessandro di Casalpusterlengo (LO))
a) Nel quadrato le diagonali sono isometriche e si dimezzano.
Dalle 2 diagonali il quadrato viene diviso in 2 triangoli rettangoli isosceli congruenti
in cui AM e AN sono una mediana [sono mediane]; 1/2 [meta'] diagonale (BO) è la mediana
relativa al lato AC (l'altra diagonale ); quindi i punti L e S in cui la diagonale viene
divisa dai segmenti condotti da A sono il baricentro del triangolo (ABC)[e del triangolo
(ADC)].
Secondo una proprietà delle mediane, il baricentro divide la mediana stessa in 2 segmenti
di cui quello verso il vertice è doppio dell'altro per cui BL= 2*OL ; ma OL = OS e si
verifica allora che BL = DS = SO + OL. E quindi i tre segmenti risultano congruenti.
b) Vale per tutti i parallelogrammi perchè in essi le diagonali si dimezzano e dividono[ciascuna divide] la figura in 2 triangoli congruenti.
---------------------------------------------------------
Soluzione di Valentina Rosa, Pirrone Domenico della SMS Enrico Panzacchi - OZZANO EMILIA (BO)
Se consideriamo i due triangoli rettangoli ABM e AND, possiamo affermare che sono
congruenti perche' AB corrisponde [e' congruente]a DA e MB a DN e l'angolo tra essi e' in
tutti e due i casi di 90 gradi.
Quindi questi due triangoli sono congruenti per il primo criterio di congruenza e MA e'
congruente a NA.
Concentriamoci adesso sui triangoli EBM e DFN. Di essi sappiamo che MB=DN e che gli angoli
B e D sono di 45 gradi perche' la diagonale del quadrato taglia a meta' l'angolo di 90
gradi.
Possiamo anche dire che [l'angolo] M=N grazie alle figure prese in considerazione prima.
Se due angoli sono congruenti [[per forza]] anche il terzo e' uguale. I 2 triangoli sono
congruenti per il secondo criterio di congruenza dei triangoli.
Quindi EB e' congruente a DF.
Per dimostrare che anche FE e' congruente a EB e DF guardiamo i triangoli DFN e FAB.
Essi hanno [l'angolo]N=A perche' alterni di rette parallele DC e AB tagliate dalla
trasversale AN.
B=D per lo stesso motivo, ma con trasversale BD e DFN e AFB sono uguali perche' opposti al
vertice quindi i 2 triangoli sono simili con R= 1/2 perche DN= 1/2 AB per costruzione.
Quindi DF= 1/2 FB.
Ma FB= FE+EB sostituisco [FB=]FE+DF quindi FE= EB= DF.
-----------------------------------
Arrivederci a Dicembre con il prossimo problema!
Giuliana BETTINI - Franca NOE' - Consolato PELLEGRINO
| Il problema | Come partecipare | | Archivi | Calendario | | Scuole | | Altri problemi |