FLATlandia

Marzo 1999

Il testo del problema:

a) Dimostrare che la bisettrice di un angolo è l'asse di una simmetria che trasforma ciascun punto di un lato dell'angolo in uno dell'altro lato.

b) Dati:
- tre rette che concorrono in un punto I;
- un punto A su una di esse;
costruire un triangolo che ha tali rette come bisettrici e uno dei suoi vertici in A.
Esiste sempre una soluzione? E' unica?

Motivare la costruzione e giustificare le risposte.

Soluzioni

Premessa:

Abbiamo ricevuto sette risposte provenienti da sette scuole di cui quattro sono Scuole Medie Inferiori. Sono inoltre pervenute tre figure realizzate da una classe quinta di una scuola elementare (la stessa che ha partecipato il mese scorso).

Il problema di questo mese chiedeva di dimostrare una proprietà della bisettrice di un angolo e poi di costruire un triangolo soddisfacente certe condizioni. L'utilizzo della suddetta proprieta' facilita la realizzazione della costruzione richiesta.

In nessuna delle risposte sono stati risolti in modo esauriente tutti i quesiti posti dal problema.

A tutti i ragazzi, ed in particolare a quelli che usano Cabri, ricordiamo che: - una o piu' verifiche di un teorema o di una congettura, non e' una dimostrazione e quindi la prova di "trascinamento" non è sufficiente per confermare e giustificare la bontà di una costruzione realizzata con Cabri; - le figure ottenute con un "aggiustamento" non sono vere e proprie costruzioni (nella geometria razionale sono bandite le costruzioni "ad occhio", che oltretutto non resistono alla prova "trascinamento"); -il testo della risposta non deve essere scritto nel file della figura, ma va inviato o come file Word o meglio (per facilitarne la diffusione) su un semplice messaggio e-mail.

Le scuole che hanno partecipato sono:

Sc.El. "Villaggio Europa" (Dir.Did.II Circolo), Alessandria; SM "Luca Valenziano", Tortona (AL); SM "Cerreta", Bologna; SM "G. da Cermenate", Cermenate (CO); SM di Roveredo in Piano (PN); ITG "Rondani" Parma; ITI "Euganeo", Este (PD); LS "G. Galilei", Bitonto (BA).

Abbiamo composto una soluzione completa del problema scegliendo le parti migliori fra le risposte provenienti da: SM "Valenziano" (prima parte), ITG "Rondani" (seconda parte), SM "Cerreta" (ultima parte).

NOTA 1: Nelle soluzioni riportate le correzioni o i commenti al testo sono fra parentesi quadre.

NOTA 2: Chi invia il testo o le figure in attachment e' pregato di assegnare ai file nomi piu' caratterizzanti di un generico Flat, Flat1, Flat11: alla fine, nel computer che riceve le risposte finiscono tutte in una stessa cartella ed e' difficile distinguerle fra loro.

NOTA 3: Vi preghiamo di non dimenticare le indicazioni richieste nel regolamento (nome e (o) classe, scuola, localita').

Soluzione della parte a) del problema proposta da:

De Icco Roberto, Dossola Stefano e Merli Marco

Classe 2°D t.p. della Scuola Media Statale "Luca Valenziano" di Tortona.

Consideriamo l'angolo AOB e la sua bisettrice b. Prendiamo un punto qualsiasi P su OA e mandiamo la perpendicolare da P alla bisettrice. Indichiamo con H il punto di intersezione della perpendicolare con b e con Q quello della perpendicolare con l'altro lato OB. Dimostriamo che PH=QH. Infatti i triangoli OHP e OHQ sono congruenti perche' hanno OH in comune, l'angolo POH=HOQ perche' meta' dell'angolo AOB ed hanno un angolo retto. Quindi P e Q si corrispondono in una simmetria di asse b.

Soluzione del problema proposta da:

Marco Moia

Classe 2°I - ITGS "Rondani" , Parma

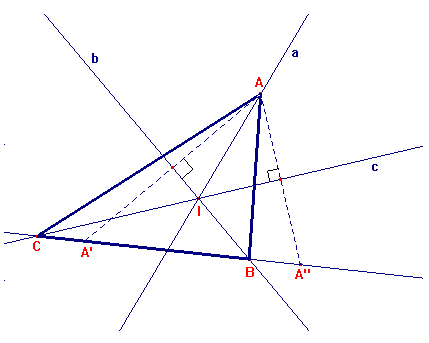
Per poter effettuare la costruzione sopra riportata [si fa riferimento ad una figura in cui r, s, t sono le tre rette che concorrono in I, A appartiene alla retta s], ci dobbiamo aiutare con la dimostrazione fatta in precedenza, e quindi, grazie agli strumenti di Cabri 2, determiniamo il simmetrico del punto dato A, usando come asse di simmetria la retta r, e ripetiamo successivamente l'operazione ma usando questa volta, la retta t. Questi due procedimenti ci permetteranno di determinare i punti H e K che a loro volta determinano la retta sulla quale si trova la base del triangolo che dovremo andare a costruire. Determiniamo ora i punti B e C, intersezioni tra la retta appena individuata e le rette t ed r. I punti A, B e C costituiscono ora i vertici del nostro triangolo, ora non ci resta che unire i tre vertici ed otterremo un triangolo che ha come lati i segmenti AB, AC e BC e come bisettrici le tre rette date.

Tuttavia, non esiste sempre una soluzione a questo problema. Infatti, se la retta passante per H e K si trova al di sopra dell'incontro delle tre rette (incentro del triangolo), la costruzione non rispetterà i criteri preposti. Infatti in un qualsiasi triangolo, l'incentro è sempre interno al triangolo stesso. La posizione della retta passante per H e K, è inoltre determinata dalla misura degli angoli che le due rette (r e t) vengono a formare incontrandosi. Se infatti, questi angoli [quelli che non contengono la retta s] misurano più di 90° [o sono uguali a 90°], la nostra soluzione non potrà esistere.

Possiamo inoltre affermare che date tre rette che si incontrano in un punto, e dato un punto A su una di esse, la soluzione al nostro problema [se esiste] sarà unica.

Soluzione del problema proposta da:

Laura Campogrande, Elisabetta Cocco, Irene Gualandi, Laura Incorpora, Elena Manenti

Classe III - Scuola Media "Cerreta", Bologna.

[Si fa riferimento al triangolo gia'costruito in cui si indica con a l'angolo acuto formato dalle bisettrici degli angoli di vertici C e B; con b quello delle bisettrici di A e C e con c quello delle bisettrici di A e B] Indicando con x meta' dell' angolo BAC, y meta' dell' angolo ACB e con z meta' dell' angolo CBA (per definizione di bisettrice) troviamo il loro valore in funzione degli angoli a, b, c tra le tre bisettrici in I. Sapendo che la somma degli angoli interni di un triangolo è di 180°, consideriamo il triangolo AIC: y=180-x-(a+c).
Consideriamo il triangolo BIC: z= 180-(b+c)-[180-x-(a+c)]=x+a-b Consideriamo il triangolo BIA: x+a-b+x+a+b=180, cioe' x=90-a. Sostituendo nelle equazioni precedenti, troviamo y=90-c, z=90-b; con a+b+c=180°.
Ne deduciamo che il triangolo si può costruire solo se a, b, c <90°.

| Home Page Cabri | Torna a FLATlandia | Archivi |