FLATlandia

Febbraio '99

Il testo del problema:

a) Costruire un quadrilatero ABCD, diviso dalla diagonale AC in due triangoli congruenti.

1) Quali e quanti tipi di quadrilateri si possono ottenere? Motivare le risposte.
2) Dimostrare che in ognuno dei casi individuati la retta AC dimezza la diagonale BD.
3) Le figure ottenute presentano delle simmetrie?

b) Come possono variare i vertici B e D se vogliamo ora che il quadrilatero ABCD sia diviso dalla retta AC in due triangoli equivalenti? In tal caso che cosa succede alla diagonale BD? Giustificare le risposte.

Soluzioni

Premessa:

Abbiamo ricevuto undici risposte provenienti da otto scuole di cui una sola è una Scuola Media Inferiore ed inoltre ci è pervenuta una figura proveniente dalle classi quinte di una scuola elementare (benvenuti nel mondo di Flatlandia!).

Due risposte non sono accettabili: una perchè non fornisce né costruzioni né motivazioni nella prima parte (che contiene anche affermazioni non pertinenti) e non ha recepito la richiesta del problema nella seconda parte; l'altra non fornisce alcun criterio di costruzione delle figure e non chiarisce quali siano le ipotesi delle dimostrazioni successive, confonde le caratteristiche di simmetria dei parallelogrammi e dei romboidi (deltoidi) e dà una motivazione completamente errata nella seconda parte.

Anche nella maggioranza delle risposte accolte la costruzione delle figure è solo accennata o descritta in modo incompleto.
Il problema chiedeva esplicitamente di costruire quadrilateri con una particolare caratteristica e di indagare poi su una loro proprietà e su
eventuali simmetrie.
Chi ha utilizzato subito il concetto di simmetria per fare le figure doveva ugualmente descrivere le costruzioni e non rimandare alle figure già fatte. Ricordate che nelle comunicazione via mail non possiamo riportare le figure!!

Abbiamo riscontrato in generale un buon livello nella esposizione, speriamo anche in una piu' precisa attenzione ai contenuti.

Le scuole che hanno partecipato sono:

Sc.El."Villaggio Europa" (Dir.Did.II Circolo) Alessandria
S.M. "Luca Valenziano" Tortona AL
L.G. "Concetto Marchesi" Oderzo TV
I.P.S.A.R. "Pellegrino Artusi" Forlimpopoli FO
LS "Francesco d'Assisi" Roma
I.T.I. "Euganeo" Este
L.S. "Galileo Galilei" Adria RO
L.S.T. "Cesaris" Casalpusterlengo LO
I.T.I. "Einaudi-Galilei" San Giovanni in Persiceto BO

Abbiamo scelto di riportare via e-mail la risposta dell'I.T.I. "Euganeo" per la completezza dei casi osservati; la risposta dell'I.P.S.A.R. "Artusi", anche se incompleta nella seconda parte, perchè descrive in modo esauriente le costruzioni; infine la prima parte della risposta inviata dalla Scuola Media (la seconda parte non è accettabile) per testimoniare l'apprezzabile livello di preparazione della classe che l'ha inviata.

NOTA 1: Nelle soluzioni riportate le correzioni o i commenti al testo sono fra parentesi quadre.

NOTA 2: Chi invia il testo o le figure in attachment è pregato di assegnare ai file nomi più caratterizzanti di un generico Flat, Flat1,
Flat11: alla fine, nel computer che riceve le risposte finiscono tutte in una stessa cartella ed è difficile distinguerle fra loro.

NOTA 3: E' arrivata con notevole ritardo una risposta proveniente dal Liceo scientifico "M. Morandi" Finale Emilia (Modena). Vi invitiamo ad essere più puntuali.

Soluzione proposta da:
Federica Lunardi e  Anna Peruffo
Classe 1° B st, indirizzo Scientifico-Tecnologico - ITIS "EUGANEO" - ESTE

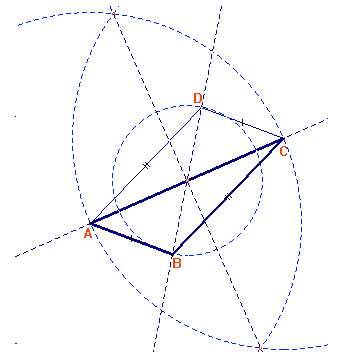
1) Si può ottenere un parallelogramma ottenuto dal triangolo ABC, il cui lato AB viene traslato nella retta parallela ad AB passante per C.
Congiungendo D con A otteniamo un parallelogramma che può essere rettangolo, se gli angoli sono retti; quadrato se gli angoli sono retti e i lati uguali, rombo se i lati sono uguali. Questa figura presenta la simmetria centrale con centro il punto di intersezione delle diagonali
(quindi la diagonale maggiore AC dimezza quella minore DB).

2) Partendo dal triangolo ABC con una simmetria di asse AC costruisco il quadrilatero (romboide [deltoide]). Questo romboide [deltoide] può essere formato da due triangoli isosceli ABD e BDC da cui si possono ottenere due situazioni:
- Se il punto d'intersezione O delle diagonali AC e BD coincide con A si forma un triangolo isoscele, che rappresenta il massimo limite (si ha quando il triangolo ABC è retto in A, AC e AB sono i cateti, e CB è l'ipotenusa);
- Se il punto d'intersezione O delle diagonali AC e BD è esterno al segmento AC si forma un quadrilatero non convesso.
- Se il punto d'intersezione O delle diagonali AC e BD è interno al segmento AC si forma un quadrilatero convesso (romboide[deltoide]).
- La figura presenta sempre la simmetria assiale e il segmento AC dimezza sempre il segmento BD (è asse del segmento BD).

b) Per avere triangoli equivalenti, con base coincidente AC, dobbiamo avere i vertici sulle rette (b e d) parallele ad AC ed equidistanti da AC (così i triangoli hanno anche uguale altezza). In questo caso fissato il vertice B sulla retta b e preso D sulla retta D, posso muovere D sulla retta d e osservo che il segmento DB è formato dai due segmenti che sono le ipotenuse di due triangoli rettangoli che hanno un cateto uguale (la distanza tra le due rette parallele) e gli angoli acuti uguali (i due opposti al vertice, i due retti e gli altri acuti uguali).

Soluzione proposta da:
Classi 2A e 2B
IPSSAR "Pellegrino Artusi", Forlimpopoli (FO)

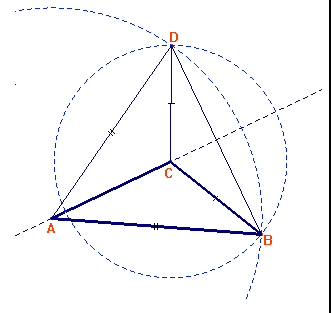
a) Partendo da un triangolo (qualunque) ABC esistono due metodi per ottenere un quadrilatero con le caratteristiche richieste. Il primo metodo (fig. 1) consiste nel tracciare la parallela ad AB passante per C e la parallela a BC passante per A e dopo aver chiamato D il punto di intersezione di tali rette si costruiscono i segmenti AD e CD.
Il secondo metodo (fig. 2) è il seguente: si traccia la perpendicolare alla retta AC passante per B e si chiama O il punto di intersezione delle due rette. Si traccia poi la circonferenza di centro O e raggio OB e si chiama D il punto di intersezione di questa circonferenza con la retta OB. Successivamente si costruiscono i segmenti AD e CD.

1) Col primo metodo si ottiene un parallelogramma che, in casi particolari, può essere un rombo, un rettangolo o un quadrato. Nel secondo caso si ottiene un quadrilatero con le diagonali perpendicolari che può essere convesso se entrambi gli angoli in A e in C sono acuti oppure concavo se uno dei due angoli è ottuso.
Nel caso in cui uno dei due angoli sia retto la figura non è un quadrilatero ma un triangolo. In totale, quindi, sei tipi di quadrilateri.

2) Nel caso in cui il quadrilatero sia un parallelogramma, la diagonale BD è divisa a metà dalla retta AC per una proprietà delle diagonali di un parallelogramma.
Nel secondo caso, invece, OB e OD hanno la stessa lunghezza in quanto raggi della stessa circonferenza.

3) Il parallelogramma presenta una simmetria centrale con centro il punto di intersezione delle diagonali. Il quadrilatero con le diagonali
perpendicolari (sia esso concavo o convesso) presenta una simmetria assiale con asse la retta AC.

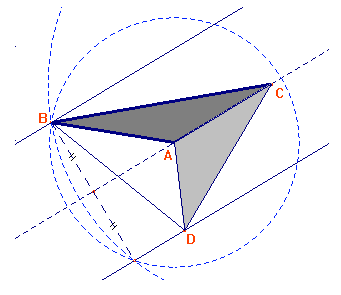
b) Si consideri il quadrilatero ABCD e si costruiscano le rette parallele ad AC passanti per B e per D. I punti B e D possono muoversi liberamente su tali parallele in quanto i triangoli ACB e ACD hanno la base AC in comune e le altezze di uguale lunghezza per cui hanno la stessa area (fig. 3).
Nel caso in cui uno degli angoli interni BAD o BCD abbia un'ampiezza maggiore di 180 gradi; il quadrilatero ABCD risulta concavo e la diagonale BD non interseca l'altra diagonale AC [ma interseca la retta AC].
[Manca la dimostrazione che AC dimezza BD]

Soluzione proposta da:
Classe II D t.p.
Scuola Media Statale "L. Valenziano" di TORTONA (AL).

a) Abbiamo preso in considerazione 2 ipotesi:
1° ipotesi : lati consecutivi congruenti:AD=AB e DC=BC. Il quadrilatero ABCD è un deltoide. AC è asse di simmetria. Detto H il punto di intersezione delle diagonali , DH=HB perchè i punti D e B si corrispondono in tale simmetria.
2° ipotesi : lati opposti congruenti: AD=BC e DC=AB. Il quadrilatero ABCD è un parallelogrammo. In un parallelogrammo le diagonali si dimezzano e il loro punto di intersezione è centro di simmetria.

Giuliana BETTINI
Franca NOE'
Consolato PELLEGRINO

| Home Page Cabri | Torna a FLATlandia | Archivi |