 FLATlandia
FLATlandia FLATlandia
FLATlandia
Dicembre '98
Il testo del problema:
Data una circonferenza C ed un punto P interno ad essa, costruire (con riga non graduata e compasso) un triangolo equilatero inscritto in C con un lato passante per P.
Il problema ammette sempre soluzioni? Quante?
Soluzioni
Abbiamo ricevuto undici risposte provenienti da nove scuole, di cui quattro sono scuole
medie inferiori, ed una risposta che non e' stata valutata in quanto l'"autore"
non dichiara se e' uno studente e, in tal caso, di quale scuola e localita'.
Fra le risposte prese in esame, tre non sono state accolte per motivi di vario ordine:
Il problema richiedeva una costruzione, con riga e compasso o con un software idoneo, ed una indagine sulle sue possibilita' di realizzazione: in tutte le risposte accolte i due quesiti posti sono stati risolti in modo piu' o meno esauriente ed e' stata riscontrata una discreta correttezza nella esposizione; ci siamo quindi trovati nell'imbarazzo della scelta della risposta da presentare.
Abbiamo optato per tre risposte: la prima perche' proveniente da una scuola media inferiore, che propone la stessa costruzione di quasi tutte le altre; la seconda, inviata da una scuola media superiore, perche' anche se necessita di una nota chiarificatrice, ricorre ad una costruzione diversa dalla precedente, infine la terza risposta, scelta per la completezza della sua costruzione.
Le scuole che hanno partecipato sono:
NOTA: Come di consueto nelle soluzioni riportate le correzioni al testo sono fra parentesi quadre. Le parti superflue sono fra doppie parentesi quadre.
--------------------------------------------
Soluzione proposta dalla classe 2^ D t.p.
Scuola Media St. "Luca Valenziano" di Tortona (AL)
Data una circonferenza C di centro O e raggio r, il lato del triangolo equilatero
inscritto in C ha distanza dal centro uguale ad r/2. Il punto P allora dovrà essere tale
che r/2<=OP<=r [<r].
Costruzione del triangolo equilatero richiesto:
1) costruire la circonferenza C' di centro O e raggio r/2;
2) mandare da P le tangenti a C' ed indicare con A e B i punti di tangenza;
3) prolungare il segmento AP ed indicare con X e Y le intersezioni con C. La corda XY è
il lato del triangolo equilatero cercato. Il terzo vertice del triangolo è il punto di
intersezione con C del diametro passante per A, situato da parte opposta ad A rispetto ad
O;
4) con analoga costruzione, prolungando il segmento PB, si ottiene un' altra soluzione del
problema.
Il problema ammette dunque due soluzioni, simmetriche rispetto al diametro passante per P,
distinte se r/2<OP<r, coincidenti se OP=r/2 [[o Op=r]].
---------------------------------------------
Soluzione proposta dalle studentesse: FEDERICA LUNARDI e ANNA
PERUFFO
ITIS "Euganeo" Este (PD)
Costruisco una circonferenza c di centro O e raggio r. Trovo il punto medio del raggio
r e traccio la circonferenza di raggio OM. Inserendo [Disegnando] il triangolo equilatero
nella circonferenza c, si osserva che O e' punto d'incontro delle altezze, delle mediane,
quindi se il lato è A'B' e l'altezza relativa C'H, questa passa per O e C'O e' il doppio
di C'H (C'H = r/2). Se costruisco il cerchio di raggio r/2 e centro in O, ogni lato del
triangolo inscritto in c risulta tangente (perpendicolare al raggio) alla circonferenza di
raggio r/2. Quindi il punto P per appartenere al lato del triangolo equilatero deve essere
all'interno della corona circolare (cioe' alla parte di cerchio grande non comune al
cerchio piccolo). Se prendo P all'interno del cerchio piccolo (di raggio r/2) non
esistera' il triangolo equilatero.
Inserisco il punto P all'interno del settore circolare (ho disegnato un punto sulla
ciconferenza grande, ho disegnato il segmento che unisce questo punto con O, ho fatto
l'intersezione con la circonferenza piccola, ho costruito il segmento che unisce i due
punti sulle circonferenze e ho inserito P su questo segmento, cosi' sono sicura che P e'
interno alla corona circolare). Traccio la circonferenza di raggio PO e trovo i punti di
intersezione con la circonferenza c. Da uno dei due punti (quindi i triangoli che posso
costruire sono due), che ho chiamato S, traccio la circonferenza di raggio SO e trovo
l'intersezione con la circonferenza c.
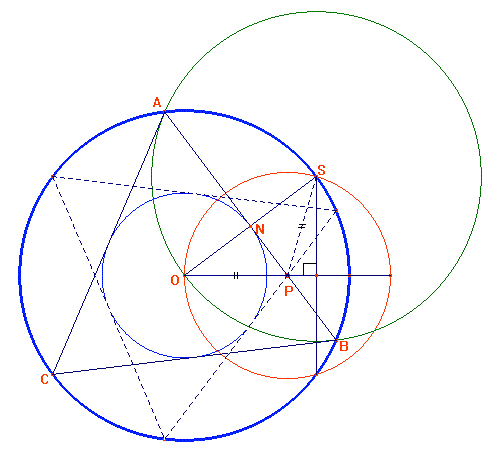
Chiamo i due punti A e B. Il segmento che unirà i due punti sara' un lato (passante per
P) del triangolo. Trovo il punto medio di AB che chiamo N, traccio la perpendicolare ad AB
passante per N, passa per il centro O e interseca la circonferenza nel punto C.
[Nota: la costruzione e' valida perche' in questo modo il punto P
appartiene all'asse di OS, come evidenziato nella figura.]
Ho realizzato il lavoro con CABRI.
Verifica al VIDEO: Se clicchiamo sul punto P e lo spostiamo all'interno della corona
circolare c'e' sempre la costruzione del triangolo equilatero; appena sposto P all'interno
della circonferenza di raggio MO, il triangolo sparisce perche' non esiste.
---------------------------------------------
Soluzione proposta dalla classe II sez. E
ITG "Buonarroti" - Caserta
Con riferimento alla figura , si vuole riportare la soluzione del quesito proposto in questo mese.
Dal punto P, interno al cerchio, si mandano le rette tangenti alla circonferenza c2, concentrica alla data circonferenza c1, ma di raggio r2, uguale alla metà del raggio (diciamolo r1) della circonferenza assegnata c1. Detti A,B e A’,B’ i punti di intersezione di dette tangenti con la c1, da essi si tracciano le tangenti alla c2 ( tali tangenti hanno dal centro O una distanza pari ad r1/2, ovviamente). I due triangoli (ABC) e (A’B’C’) risultano equilateri per avere i tre lati uguali, ognuno pari a r1*(radice quadrata di tre), come facilmente si può calcolare, applicando il teorema di Pitagora al triangolo rettangolo OHB’, retto in H. OB’(ipotenusa) è il raggio r1 della circonferenza c1, mentre OH è di misura r1/2.
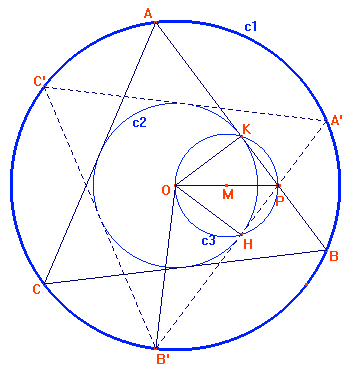
Diciamo d la distanza del punto P dal centro O della circonferenza c1; se è d< r1/2, non esistono triangoli equilateri soddisfacenti le condizioni poste dal quesito; se è d=r1/2, allora la soluzione esiste ed è unica, perché è unica la retta tangente alla circonferenza c2, condotta da P, che in questo caso appartiene alla c2; se è r1/2 < d < r1 allora le soluzioni sono due (è il caso della figura sopra riportata).
La circonferenza c3, rappresentata in figura, serve alla costruzione delle rette tangenti alla c2 condotte da P.
| Home Page Cabri |