FLATlandia

Aprile 1999

Il testo del problema:

1. Disegna su un foglio un triangolo equilatero ed esternamente ad esso, con ipotenusa su ciascun lato, un triangolo rettangolo isoscele. Ritaglia ora lungo il bordo la figura ottenuta e, piegando lungo i lati del triangolo equilatero i tre triangoli isosceli, costruisci una piramide. Sai indicare qualche proprietà di questa piramide?
2. Considera come base della piramide il triangolo equilatero e calcola in funzione del lato "l" di detta base la lunghezza di ciascuno spigolo laterale e dell'altezza della piramide.
3. Se i tre triangoli isosceli, congruenti tra loro, costruiti sui lati del triangolo equilatero sono acutangoli si ottiene ancora una piramide? E se sono ottusangoli?

Giustificare le risposte.

Soluzioni

Premessa:

abbiamo ricevuto nove risposte provenienti da sette scuole di cui due sono Scuole Medie Inferiori.
Anche questa volta ci sono pervenute, con ritardo, le figure inviate da allievi di una Scuola Elementare.
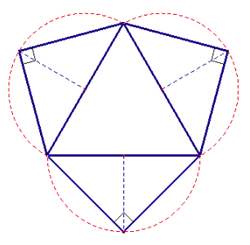
Il problema di questo mese chiedeva di costruire effettivamente il solido che si otteneva ritagliando una certa figura disegnata a partire da untriangolo equilatero fissato a piacere.
Le condizioni poste portavano in effetti ad una piramide retta regolare rispetto al triangolo equilatero assunto come base.
Il problema poi chiedeva di calcolare alcuni elementi caratteristici della piramide ottenuta e di stabilire cosa accadeva quando si modificava incerti modi la figura da disegnare.
In nessuna delle risposte sono stati risolti in modo esauriente tutti i quesiti posti dal problema.

Le scuole che hanno partecipato sono:

• S.E. "Villaggio Europa" (Dir. Did.II Circolo), Alessandria;
• L.G. "Orazio", Roma;
• L.S.T. "Cesaris", Casalpusterlengo (Lodi);
• S.M. "Cerreta", Bologna;
• S.M. "Testoni Fioravanti", Bologna;
• L.S. "Morandi", Finale E. (MO) ;
• I.T.I. "Euganeo", Este (PD);
• L.S. "G. Galilei", Bitonto (BA).

Abbiamo composto una soluzione completa del problema scegliendo le parti migliori fra le risposte provenienti da:

• SM "Cerreta" e L.C. "Orazio" (prima parte),
• LS "G. Galilei" (seconda parte),
• LT "Cesaris" (ultima parte).

NOTA: Nelle soluzioni riportate le correzioni o i commenti al testo sono fra parentesi quadre.

Risposta alla parte a) del problema

proposta da Eugenia Cammarota
classe IV Ginnasio sez. D, Liceo Classico "Orazio" - Roma

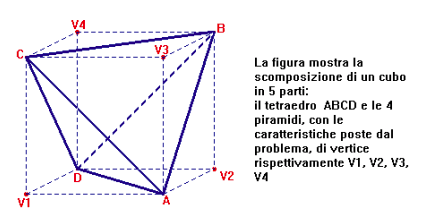
Il cubo che ha come spigolo lo spigolo laterale della piramide contiene 4 delle piramidi considerate e un tetraedro che ha come spigolo lo spigolo di base della piramide. Il volume della piramide è un sesto del volume del cubo mentre il volume del tetraedro e' un terzo.
[nei calcoli che seguono il lato l(elle) del triangolo equilatero è stato posto uguale a 1(uno)]

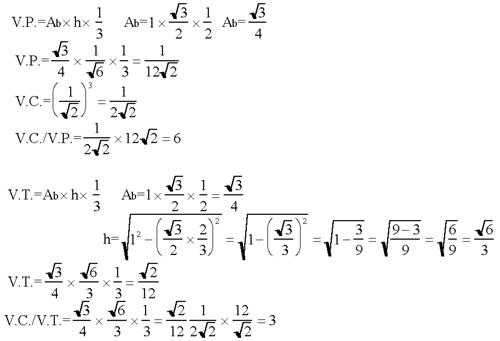
La superficie laterale della piramide è un quarto della superficie laterale [totale] del cubo.

Risposta alla parte a) del problema

proposta da Laura Campogrande, Elisabetta Cocco, Irene Gualandi, Laura Incorpora, Elena Manenti
Classe III Media, S.M. "Cerreta" - Bologna

a) La piramide risulta regolare, in quanto la base è un poligono regolare e il piede dell'altezza coincide col centro della circonferenza inscritta nel poligono di base ([infatti] le facce laterali sono congruenti e pertanto le altezze [anche le loro altezze sono] congruenti).

Risposta alla parte b) del problema

proposta da Bart Vermeulen, Vito Mastrodonato, Elio Luigi Silvestri,  Remo Infante
2^a E Liceo Scientifico "Galileo Galilei" - Bitonto (BA)

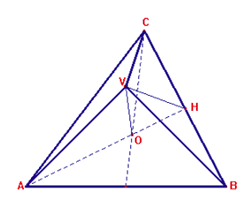
Come in ogni piramide regolare il triangolo VOP è retto in O, dove VO è l'altezza della piramide, VP l'apotema laterale, OP il raggio di base.
Se l e' la misura del lato del triangolo equilatero ABC, lo spigolo laterale della piramide, che sara' CV', misura l*sqrt (2)/2, in quanto lato del quadrato di diagonale l.
L'apotema della piramide PV' misura l/2 e l'apotema di base OP, essendo 1/3 dell'altezza di base CM, misura l*sqrt(3)/6. Applicando il teorema di Pitagora al triangolo rettangolo VOP si ottiene che l'altezza VO della
piramide misura l*sqrt(6)/6.

Risposta alla parte c) del problema

proposta da Marco Zavatarelli e Valentina Garioni
1^a Liceo Tecnologico "Cesaris" - Casalpusterlengo (Lodi)

Se i tre triangoli isosceli, costruiti sui lati del triangolo equilatero, sono acutangoli è sempre possibile ottenere una piramide.
Se i tre triangoli isosceli , costruiti sui lati del triangolo equilatero sono ottusangoli non sempre si ottiene una piramide.
La piramide non si forma se l'angolo al vertice dei tre triangoli ha ampiezza maggiore a 120°.
Invece se l'angolo al vertice e' 120° i tre triangoli si schiacciano sulla base.
Nel caso dove i triangoli abbiano l'angolo al vertice minore di 120° la costruzione e' possibile. Questo perche' la somma degli angoli al vertice delle facce laterali deve essere minore di 360°.
La piramide e' costruibile quando l'apotema e' maggiore di un terzo dell'altezza del triangolo equilatero di base.
Come si puo' vedere dal disegno nel file Cesaris.fig nel caso di angolo di 120° (piramide di altezza nulla) l'apotema sarebbe KH = (1/3)AK.
Se KH > (1/3)AH la piramide e' costruibile.

| Home Page Cabri | Torna a FLATlandia | Archivi |