Gruppo studenti "Laboratorio Metamatematica"
LS "B. Varchi" Montevarchi AR

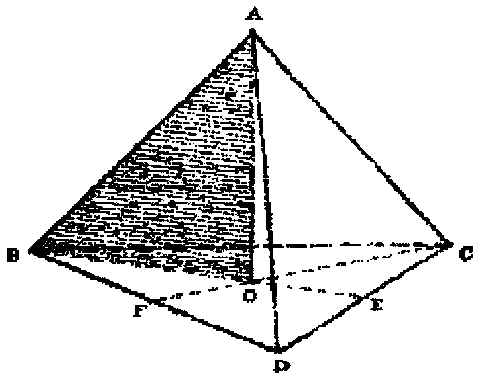
Consideriamo il tetraedro di base BCD, vertice A e spigolo s.
Sapendo che il triangolo BOA è rettangolo in O, applichiamo il teorema di Pitagora per ricavare la lunghezza del segmento AO (altezza del tetraedro). Conoscendo la lunghezza del segmento BA (spigolo del tetraedro) e potendo ricavare la lunghezza del segmento BO (2/3 dell'altezza del triangolo di base), abbiamo:
BA = s
BO = 2/3 BE, BE = (s/2) (3)1/2
dunque : BO = (s /3)(3)1/2
(BA)2 - (BO) 2= (AO)2
dunque : AO = (s /3)(6)1/2
Ricaviamo la lunghezza del raggio R della circonferenza circoscritta al triangolo equilatero ABC di lato s.
Sapendo che R corrisponde a 2/3 dell'altezza del triangolo:
R =(s/3)(3)1/2
Vediamo se è possibile, in una circonferenza di raggio
R =(s/3)(3)1/2, inscrivere un poligono regolare di lato AO = (s/3)(6)1/2.Scriviamo AO in funzione di R.
Dato che R=(s/3)(3)1/2,ne segue: s =R(3)1/2
Quindi AO = R(2)1/2
.Sapendo che R(2)1/2 è il lato del quadrato inscritto in una circonferenza di raggio R, abbiamo che il poligono regolare richiesto è un quadrato.