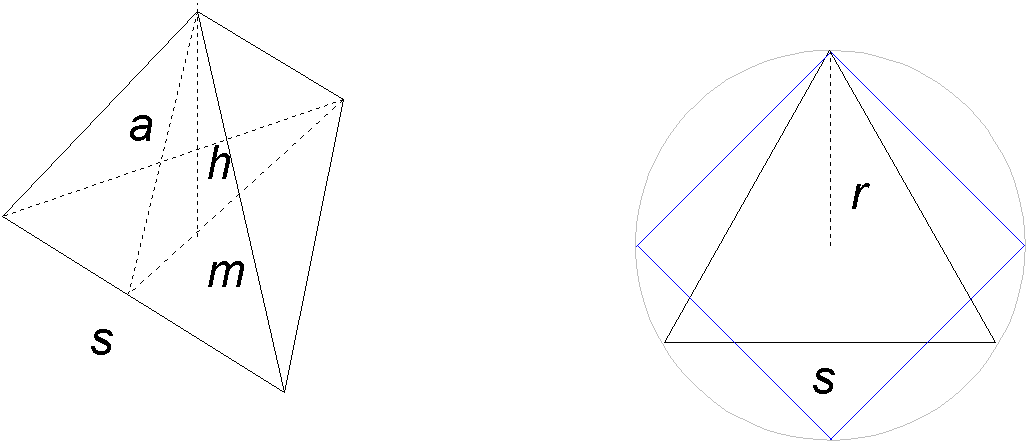
L'altezza richiesta si può calcolare applicando il teorema di Pitagora al triangolo formato dall'apotema, dall'altezza stessa e da una parte della mediana m del triangolo di base relativa allo spigolo su cui cade l'apotema:

.

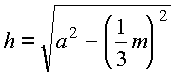Tale apotema è anche altezza della faccia a cui appartiene:

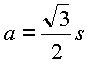
come anche m:

Sostituendo si ottiene:

.

Per il secondo quesito, si parte da una considerazione generale: data una circonferenza di raggio r, il lato del poligono regolare di n lati () misura:

.

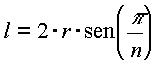In questo caso il raggio è pari ai due terzi dell'altezza del triangolo equilatero che costituisce ciascuna faccia del tetraedro:

da cui:

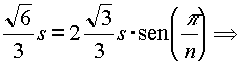
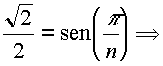
Affinché n sia intero, è necessario che il denominatore sia uguale a 1 (se fosse uguale a 2, si avrebbe n = 2, non accettabile); quindi

.

k = -1/4 non è accettabile (k è intero), quindi k = 0: n = 4.