; nel nostro caso essendo il triangolo equilatero abbiamo usato la formula
e 
.Ne è risultato che l'apotema di base è
.SCUOLA MEDIA TESTONI FIORAVANTI BOLOGNA
CLASSE 3C
Alunni: C. Falcioni, R .Mengoli, A. Paccapelo, I. Rizzo, J. Zingoni
Abbiamo considerato lo spigolo S e non un valore numerico. Abbiamo applicato la formula
per trovare l'apotema del triangolo equilatero, cioè il raggio del cerchio inscritto in
una faccia del tetraedro.
;
nel nostro caso essendo il triangolo equilatero abbiamo usato la formula
e .
Ne è risultato che l'apotema di base è
.
L'apotema del tetraedro rappresenta l'altezza del triangolo equilatero di spigolo S, cioè
.
Con questi due dati abbiamo applicato il teorema di Pitagora al triangolo di vertice OHV in cui O è il piede dell'altezza della piramide, H il piede dell'apotema, V il vertice del tetraedro
= 
= 
= 
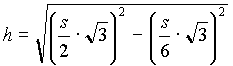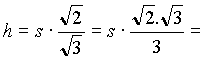
Abbiamo osservato che nell'altezza compare la 
quindi abbiamo
ipotizzato che il poligono da inscrivere nella circonferenza potesse essere un quadrato.
Secondo noi se [Poiché] il raggio della circonferenza equivale a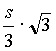 
,
il lato del poligono equivale proprio ad h, essendo il lato uguale a raggio moltiplicato
la radice di due per la nota relazione esistente tra lato e diagonale di un quadrato.