

Ruggero Giuseppe Boscovich nacque a Ragusa, in Croazia, il 18 maggio 1711, da padre serbo e madre di origine bergamasca. Sebbene il legame etnico fosse tenue, la maggior parte dell'attività del padre gesuita si svolse in Italia, e redasse in italiano molti dei suoi scritti: fu, del resto, un cosmopolita tipicamente settecentesco.
Compì i suoi primi studi presso il Collegium Ragusinum della sua città, per poi trasferirsi, una volta diventato novizio, a Roma. Ancora studente di teologia, tenne presso il Collegio Romano la cattedra di logica e matematica che era stata di Orazio Borgondio (1675-1741). Furono anni d'intensa assimilazione delle teorie di Newton e dei suoi continuatori inglesi e francesi: infatti, Boscovich fu il più deciso e profondo sostenitore del newtonianismo nell'ambiente del Collegio Romano.
Nel frattempo, il nuovo papa Benedetto XIV aveva promosso un vivace rinnovamento scientifico e culturale: quando, nel 1744, Boscovich pronunciò i voti sacerdotali di padre gesuita, godeva già di un'ottima reputazione a livello europeo. Possiamo considerare il cardinale Silvio Valenti Gonzaga (1690-1756) come il suo patrono.
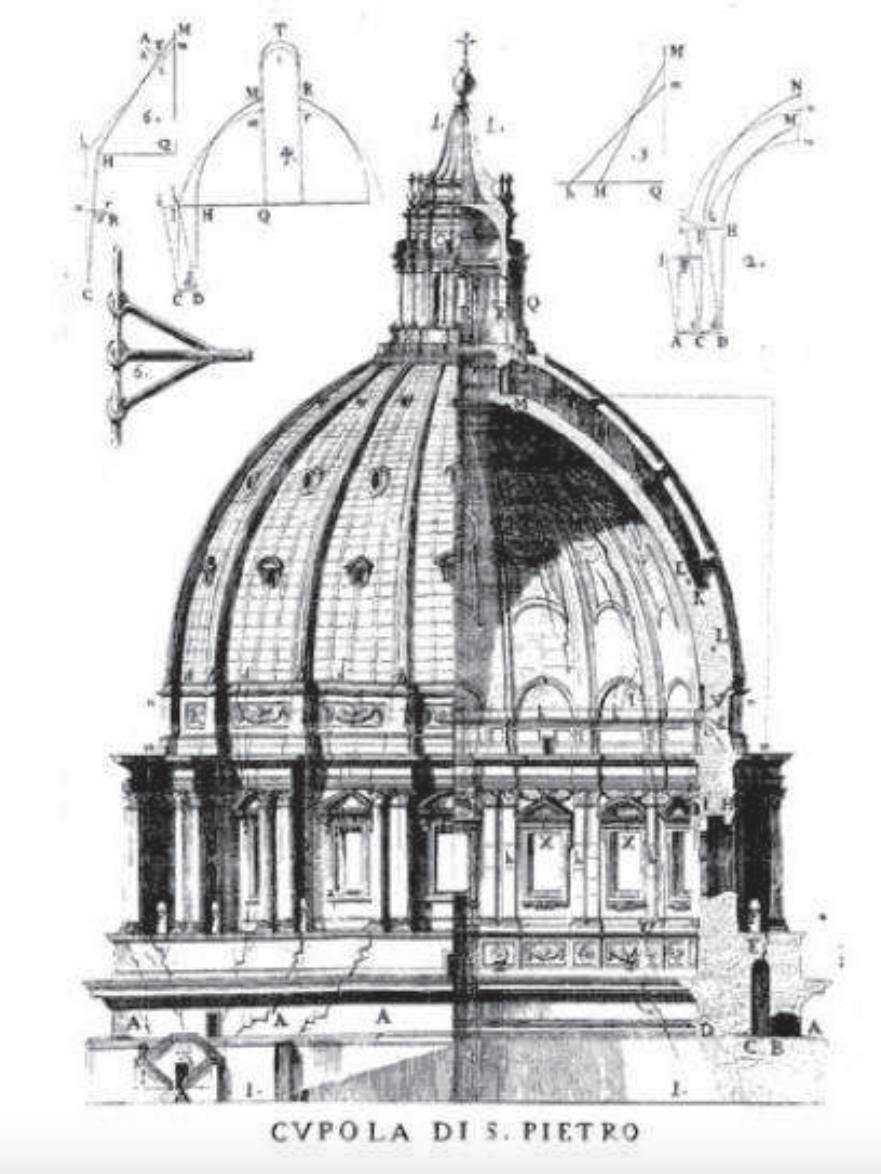
Nel 1742 fu invitato, insieme ai commentatori francesi di Newton, Thomas Le Seur (1703-1770) e François Jacquier (1711-1788), a esaminare i sintomi di crollo che presentava la cupola di S. Pietro. Ne risultarono il Parere di tre matematici sopra i danni che si son trovati nella cupola di S. Pietro in sul fine del 1742 (Roma 1742) e le Riflessioni de' pp. Tommaso Le Seur, Francesco Jacquier... e R. G. Boscovich sopra alcune difficoltà spettanti i danni, e risarcimenti della cupola di S. Pietro (ibid. 1743), contenenti un progetto d'ingegneria.
Anche negli anni successivi, Boscovich continuò, come professore di matematica presso il Collegio Romano, a pubblicare dissertazioni d'argomento fisico e meccanico, geodetico e astronomico, in alcune delle quali delineò le tesi teoriche newtoniano-leibniziane che avrebbe poi posto alla base del suo opus maius di filosofia naturale.
Ma la versatilità dell'autore non si limitò alla fisica e alla matematica. Nel 1745, in vacanza estiva a Frascati, si interessò a un ritrovamento archeologico e lo descrisse nei due saggi D'un'antica villa scoperta sul dosso del Tuscolo e D'un antico orologio a sole e di alcune altre rarità....
La fama di Boscovich era in costante ascesa: vari periodici esteri ripubblicavano i suoi saggi scientifici. Nel 1746, fu eletto socio dell'Accademia di Bologna e, nel 1748, divenne socio corrispondente dell'Académie Française.
Boscovich accettò di compiere una spedizione scientifica per stendere la mappa degli Stati della Chiesa. Diede contributi originali alla soluzione del problema newtoniano della forma della Terra, implicante varie questioni geodetiche, matematiche e astronomiche. I risultati ottenuti furono pubblicati nel resoconto del 1755 De litteraria expeditione per pontificiam Ditionem ad dimetiendos meridiani gradus et corrigendam mappam geographicam.
Nel 1754, compì il manuale Elementorum matheseos ad usum studiosae iuventutis, i cui primi due volumi sono dedicati alla geometria elementare, all'aritmetica e alla trigonometria piana e sferica; il volume terzo contiene la parte più originale, ossia la trattazione delle sezioni coniche e delle trasformazioni geometriche.
L'opera Philosophiae naturalis theoria redacta ad unicam legem virium in natura existentium (1758) è una sintesi del lavoro fisico-matematico svolto in circa tredici anni. Ne risultò uno sforzo geniale, ma prematuro e caduco, di interpretare, alla luce di un'unica formula, il mondo ancora inviolato delle particelle elementari.
Tra il maggio e il dicembre 1760 fu in Inghilterra: visitò Oxford, Cambridge e l'osservatorio di Greenwich. A Londra incontrò i maggiori intellettuali dell'epoca ed ebbe intense relazioni con ecclesiastici, diplomatici, politici. Onorevolmente accolto dagli scienziati inglesi, entrò a far parte della Royal Society nel gennaio del 1761.
Nel dicembre del '60, lasciò Londra diretto a Costantinopoli con l'incarico di osservare, per conto della Royal Society, il transito di Venere attraverso il disco solare, previsto per il settembre '61. Descrisse il viaggio nel Giornale di un viggio da Costantinopoli in Polonia(1763), ricco di concrete osservazioni sui costumi ed ordinamenti civili dei paesi slavi. Per motivi di salute e forse anche politici, tornò a Roma nel settembre '63.
Eletto professore di matematica e astronomia nell'università di Pavia, vi insegnò tra il 1764 e il 1768, quando fu trasferito alle Scuole Palatine di Milano, dove aveva intrapreso la costruzione del nuovo osservatorio di Brera. Le sue molteplici attitudini di ingegnere, matematico e astronomo gli consentirono di attrezzare uno dei più moderni istituti del genere. Ma, accusato di eccessive spese e di scarsa attitudine all'osservazione, si dimise dalla carica onorifica e dall'insegnamento.
Il 1773 fu anche l'anno dell'abolizione dell'ordine dei gesuiti, così il 21 agosto si trasferì a Parigi, dove occupò la carica di direttore dell'ottica per la marina.
Nel 1782, tornò in Italia in temporaneo congedo, ma vi avrebbe trascorso i suoi ultimi anni. Lo scarso successo di alcune sue opere, i postumi di una trombo-flebite e l'aggravamento di una psicosi depressiva lo colpirono duramente. Morì a Milano il 13 febbraio 1787 di edema polmonare e fu sepolto in S. Maria Podone.




La riflessione di Boscovich sulle sezioni coniche parte dalla lettura di una nuova edizione in 3 volumi, stampata tra il 1739 e il 1742, dell'opera Principia di Newton dei due autori francesi Minims Thomas Le Seur (1703-1770) e François Jacquier (1711-1788), che Boscovich incontra proprio a Roma. Nel trattato De Motu Corporis attracti in centrum (1743), Boscovich definisce le sezioni coniche assegnando la direttrice, il fuoco e un rapporto dato, ovvero l'eccentricità:
Una sezione conica è il luogo dei punti le cui distanze da una retta data (la direttrice) e un punto fissato (il fuoco) sono in rapporto dato.
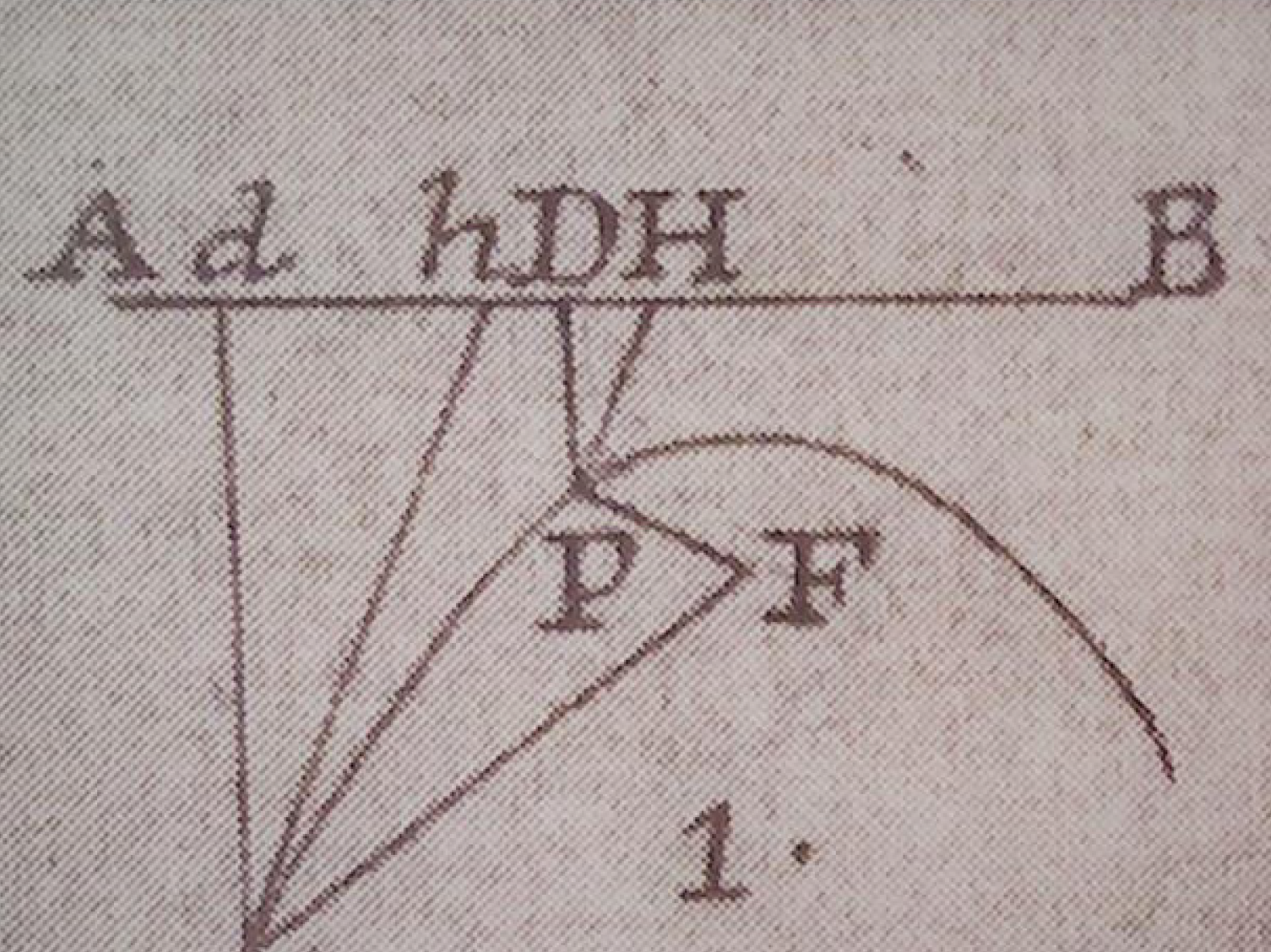

Boscovich dimostra un corollario che sarebbe diventato importante nel suo nuovo approccio alle sezioni coniche, ovvero:
Supponiamo che una corda AB incontri la direttrice ER in E. Congiungiamo E con il fuoco F e tracciamo la parallela a EF passante per A. Se H è il punto in cui tale parallela interseca il raggio focale FB, allora FA = FH.
Si rende disponibile la costruzione interattiva su Geogebra.
In seguito a questo corollario, Boscovich dimostra vari risultati. Per esempio, determina la direttrice dati il fuoco e tre punti della curva e mostra come trovare la tangente ad un punto qualsiasi della curva.
Boscovich continua a leggere i Principia, con lo scopo "di coltivare la Geometria e promuovere l'Astronomia", come scrive nel motto che accompagna il titolo dell'opuscolo Nova methodus adhibendi phasium observationes in eclipsibus lunaribus, che pubblica nel 1744.

Proprio in quest'opera, Boscovich si riferisce al teorema delle corde come "il teorema meglio conosciuto, con cui si possono risolvere agevolmente molti problemi che a prima vista sembrerebbero complicati". Nella sezione 16, lo enuncia in questa forma:
Se due rette, parallele ad altre due rette di direzione data, si intersecano tra loro e intersecano la sezione conica, i rettangoli sotto le parti tra il punto comune e le rispettive intersezioni con la conica sono in proporzione data. Quando le due intersezioni di ciascuna retta con la conica coincidono, in modo che le secanti diventino tangenti, i quadrati delle tangenti sostituiscono i rettangoli.
Figura interattiva su Geogebra.
Sulle orme di de l'Hospital, Boscovich introduce le sezioni coniche direttamente nel piano, e poi dimostra che risultano sezioni di un cono. Tuttavia, non le definisce come de l'Hospital, ma assegnando i fuochi, la direttrice e il rapporto dato. Come lui stesso sottolinea, si tratta di una definizione "attraverso la quale tutto discende in modo semplice, anche il teorema" delle corde, che mette in evidenza nel trattato.
Il progetto di Boscovich inizia a prendere forma nel 1746, dopo aver letto le opere:


Nell'articolo del 1746 Dimostrazione facile d'una principale proprietà delle Sezioni Coniche, la quale non dipende da altri teoremi Conici; e disegno d'un nuovo metodo di trattare quella dottrina, pubblicato nel Giornale de' Letterati (Art. XIX, giugno e luglio 1746, 189-193, 241-243, 315-316), Boscovich deduce il seguente importante corollario, direttamente dalla definizione di conica:
Sia una sezione conica definita dal fuoco F e dalla direttrice PA, e sia B un punto sulla conica. Allora il rapporto tra FB e BA, dove A è il punto dove la retta di direzione data passante per B interseca la direttrice, dipende solo dalla direzione di tale retta.
Figura interattiva su Geogebra.
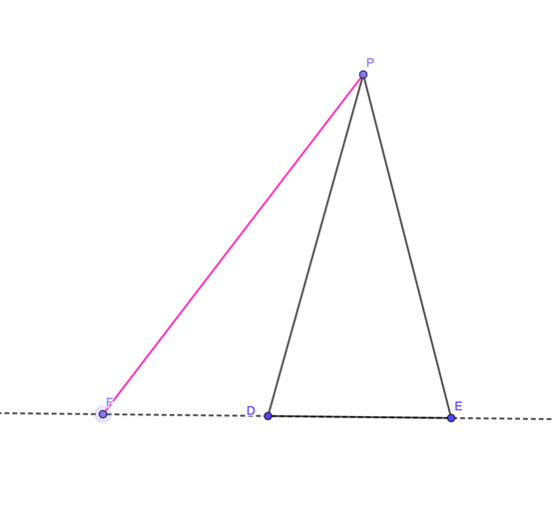
Boscovich dimostra anche il seguente fondamentale lemma:
Sia DPE un triangolo isoscele di base DE e sia F un punto sulla base, o sul suo prolungamento. Allora \(DF \times FE = |PE^2 - PF^2|\).
Semplicemente da questi risultati, ovvero dalla definizione e dal lemma, Boscovich ottiene il teorema delle corde, che ora enuncia nella forma seguente [Boscovich 1746, Teorema 1]:
Si considerino:
Allora il rapporto \(BP \times PC : bP \times Pc\) è costante.
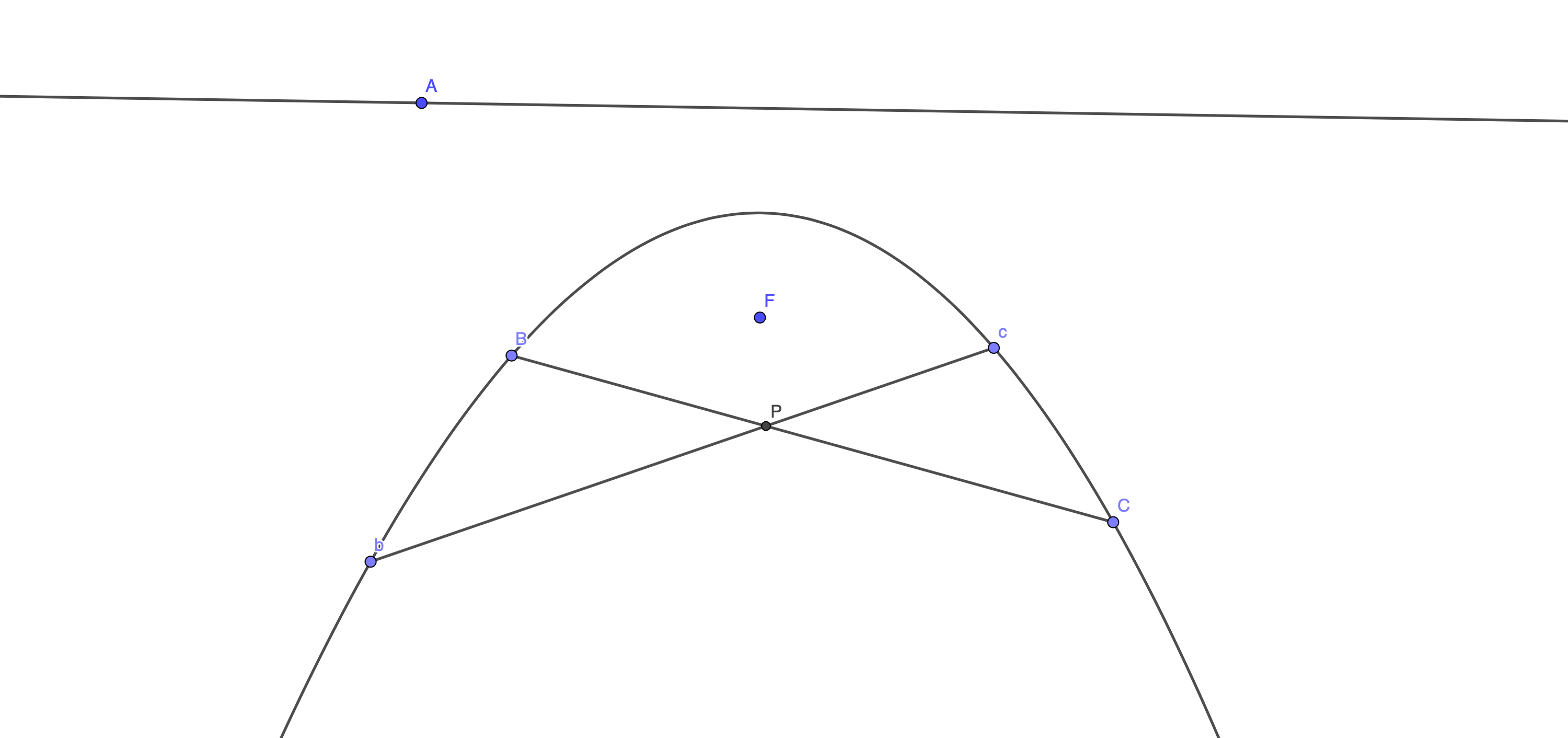
La dimostrazione è elaborata ed ingegnosa, ma completamente sviluppata sul piano. Boscovich mostra come la maggior parte delle nozioni sulle sezioni coniche può essere dedotta dal teorema appena enunciato.
L'articolo di cui abbiamo appena discusso suggerisce che Boscovich abbia già chiara la sua trattazione delle coniche nel 1746. La scoperta del cerchio eccentrico lo convince a cambiare approccio: dalla nozione di cerchio eccentrico si possono far derivare tutti i teoremi sulle coniche, attraverso opportune costruzioni geometriche. In particolare, ragiona a partire dalla definizione di sezione conica dati la direttrice, il fuoco e il rapporto dell'eccentricità, e il lemma fondamentale che abbiamo visto poc'anzi. La scoperta di questo potente strumento e il desiderio di sviluppare una teoria sulla continuità geometrica, strettamente interconnessa con la trattazione delle coniche, sono tra le ragioni per cui il terzo volume di Elementa Universae Matheseos è pubblicato in ritardo.
Nel 1754, quando viene stampato, il trattato è diviso in due parti, ciascuna con un proprio titolo:
Come scrive Boscovich nell'introduzione a Sectionum Conicarum Elementa, ci sono due modi per sviluppare la teoria delle sezioni coniche:



Il “cerchio eccentrico” viene introdotto nel terzo volume degli Elementa universae matheseos. All'inizio del trattato, Boscovich definisce una sezione conica assegnando direttrice AB, fuoco F (esterno ad AB) ed eccentricità:
Se da un punto P di una curva si traccia la retta PD perpendicolare alla direttrice AB, e si congiunge P con F, e se PF e PD hanno un rapporto costante, allora chiameremo sezione conica la curva descritta dal punto P, rispettivamente ellisse, parabola, iperbole a seconda che il rapporto sia minore, uguale o maggiore di uno.
La definizione adottata permette a Boscovich di costruire un sistema piano di coniche, cioè di trasformare una conica in un'altra, facendo variare l'eccentricità, oppure muovendo il fuoco, oppure muovendo la direttrice parallelamente a sé stessa.
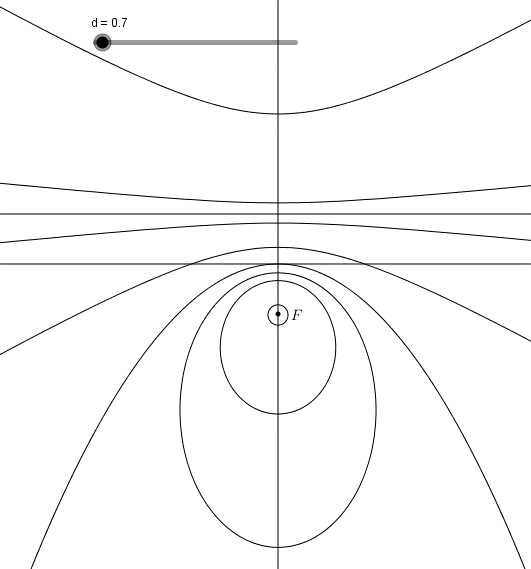
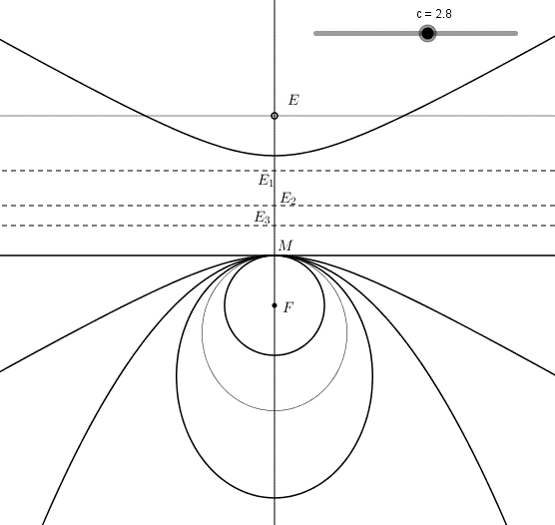
Possiamo, a questo punto, definire il cerchio eccentrico.
Data una conica, si dice cerchio eccentrico, rispetto a un dato punto, il cerchio centrato in quel punto di raggio uguale alla distanza del centro dalla direttrice della conica, moltiplicata per l'eccentricità della conica.
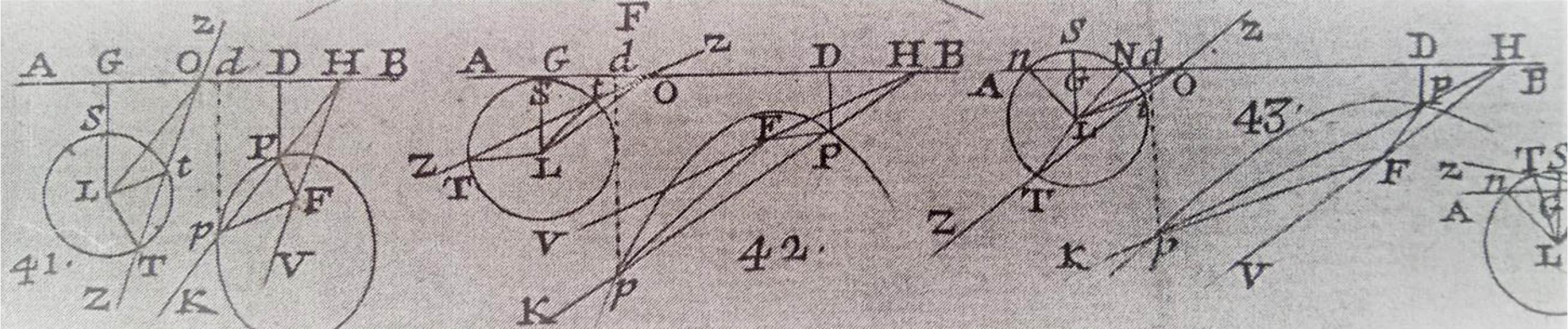
Boscovich elabora la costruzione per determinare l'intersezione di una retta HK con una conica avente fuoco F, direttrice AB, eccentricità e.
Figura interattiva su Geogebra.
Quello del cerchio eccentrico è un metodo elementare per mezzo del quale si possono ricavare dalle proprietà del cerchio le proprietà di una conica. Osserviamo che secanti e tangenti al cerchio eccentrico si trasformano in secanti e tangenti alla conica. Quindi, una retta incontra una conica al più in due punti. Inoltre:
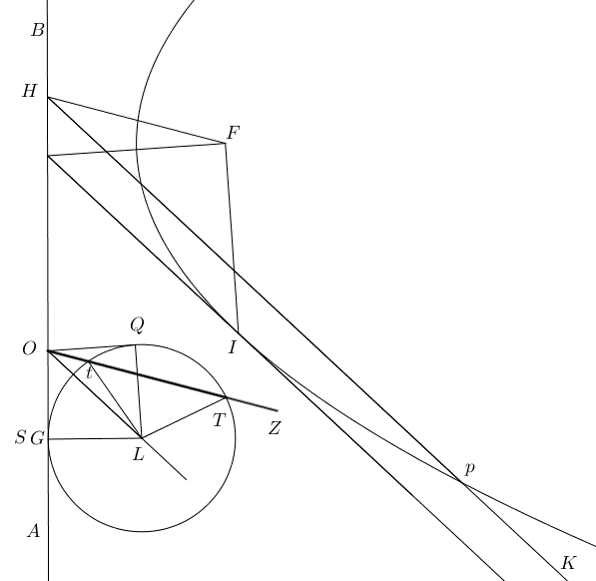
Altre Proposizioni di Boscovich che derivano dall’utilizzo del cerchio eccentrico sono le seguenti: