Le coniche secondo John Wallis
a cura di Fabio Martinelli
Scarica il testo completo e dettagliato.
John Wallis nacque il 23 novembre 1616 ad Ashford, nel Kent, e morì il 28 ottobre 1703 ad Oxford. Contribuì in modo sostanziale alle origini del calcolo e fu il matematico inglese più influente prima di Newton, suo contemporaneo. Fu studente di William Oughtred e tra gli studenti più noti di Wallis si ricorda William Brouncker.
Wallis iniziò la scuola ad Ashford, ma a causa di un'epidemia di peste si trasferì a Tenterden nel 1625, dove frequentò la scuola di grammatica di James Movat.
Trascorse il 1631-32 alla scuola di Martin Holbeach a Felsted, dove divenne esperto di latino, greco ed ebraico. Qui studiò anche logica, ma la matematica al tempo non era considerata importante come materia accademica, era vista come una disciplina meccanica, utile per l’attività di mercanti, marinai, falegnami e simili; quindi Wallis non entrò in contatto con la matematica a scuola. Fu durante le vacanze di Natale del 1631 che la conobbe per la prima volta, quando suo fratello gli insegnò le regole dell'aritmetica. Wallis scoprì di essere interessato all’argomento e cominciò a studiarlo come autodidatta, leggendo dei libri che trovava per caso dal momento che non aveva nessuno che lo guidasse nello studio.
Dalla scuola di Felsted andò all'Emmanual College di Cambridge, entrando intorno al Natale del 1632, al fine di conseguire il diploma standard di Bachelor of Arts e scelse una serie di disciplina come etica, metafisica, geografia, astronomia, medicina e anatomia. Era previsto che sarebbe diventato un medico, anche se lui non aveva mai avuto intenzione di intraprendere una tale carriera.
Nel 1637 Wallis ricevette effettivamente il diploma in Bachelor of Arts, continuò i suoi studi conseguendo il Master nel 1640 e nello stesso anno fu ordinato sacerdote. Tra il 1642 e il 1644 fu cappellano a Hedingham, Essex ed a Londra.
Questo è inoltre il periodo della guerra civile inglese, tra Realisti e Parlamentari; Wallis si schierò dalla parte dei Parlamentari ed usò le sue abilità nella crittografia per decodificare i messaggi Realisti.
Grazie a questi suoi sforzi a beneficio dei Parlamentari fu incaricato di una chiesa di Londra nel 1643. Nel 1644 Wallis divenne segretario del clero a Westminster e grazie a ciò ottenne un incarico al Queen's College di Cambridge. I suoi studi di teologia non durarono a lungo poiché nel 1645 si sposò, quindi non fu più in grado di tenere l’incarico dal momento che gli associati al College non potevano essere sposati. Tornò a Londra dove iniziò a incontrare settimanalmente un gruppo di scienziati interessati alle scienze naturali e sperimentali, gruppo che in seguito diventò la Royal Society of London.
Nel 1647 Wallis lesse il libro Clavis Mathematicae di Oughtred. Rapidamente il suo amore per la matematica, che non aveva mai trovato l'opportunità di fiorire, venne completamente alla luce. Sempre nel 1647, in seguito alla sconfitta dei Realisti ad Oxford, iniziò la cosiddetta “visita parlamentare di Oxford”, durante la quale molti professori furono deposti dalle loro cattedre e nel 1649 Wallis fu nominato da Cromwell alla Savilian Chair of geometry. Ricoprì questa cattedra ad Oxford per 54 anni, fino alla sua morte, e, anche se la sua nomina avvenne per ragioni politiche piuttosto che per merito, tale nomina si rivelò ampiamente giustificata dal lavoro svolto.
Nel 1655 e nel 1656 Wallis pubblicò due delle sue opere più importanti, rispettivamente De sectionibus conicis, nova methodo expositis ed Arithmetica infinitorum, la prima riguardante le coniche, trattate da un punto di vista innovativo, mentre la seconda è un'opera riguardante il calcolo (e comprende anche la quadratura di varie coniche).
Sebbene Wallis fosse dalla parte dei Parlamentari, si espresse contro l'esecuzione di re Carlo I e, nel 1648, firmò un documento di opposizione all'esecuzione. Sembra che ciò sia stato fatto in buona fede, non per ottenere un qualche privilegio, ma tuttavia ebbe un guadagno firmando la petizione contro l'esecuzione del re: nel 1660, quando la monarchia fu restaurata e Carlo II salì al trono, il re confermò la nomina di Wallis alla Savilian Chair. Carlo II andò anche oltre perché nominò Wallis cappellano reale e, nel 1661, lo nominò membro di un comitato istituito per rivedere il libro delle preghiere.
Durante gli anni della sua vecchiaia, Wallis pubblicò gli ultimi due volumi del suo libro Opera Mathematica, rispettivamente Opera Mathematica, volumen primum nel 1695 e Opera Mathematica, volumen tertium nel 1698 (mentre invece Opera Mathematica, volumen secundum era già stato pubblicato nel 1656) nei quali sono raccolte le sue maggiori opere. In Opera Mathematica, volumen primum compaiono i libri De sectionibus conicis, nova methodo expositis ed Arithmetica infinitorum, dei quali parleremo.
Wallis tratta le coniche nel De sectionibus conicis, nova methodo expositis (1655) e secondariamente in Arithmetica infinitorum (1656) nel quale calcola, tra le altre cose, l'area di vari segmenti conici.
Nella sua trattazione fa frequentemente uso del cosiddetto metodo degli indivisibili, la cui spiegazione ed esempi di applicazioni sono lasciati alle proposizioni I-VI.
Per capire il metodo di Wallis è importante comprendere le basi dalle quali parte, quindi prima di considerare alcune delle sue proposizioni più notevoli bisogna parlare del metodo degli indivisibili.
Il metodo degli indivisibili
E' uno strumento per calcolare aree e volumi, introdotto per la prima volta da Bonaventura Cavalieri (1598-1647) dopo il 1640 e si basa sul famoso principio di Cavalieri (="si considerino due regioni del piano comprese tra due rette parallele. Se ogni retta parallela a quelle due interseca le due regioni staccando su di esse segmenti di uguale lunghezza su entrambe le regioni, allora le due regioni hanno la stessa area", questo enunciato è in dimensione 2 ma è facilmente estendibile a spazi di dimensione superiore). Wallis però non usa il metodo tale e quale come è stato introdotto da Cavalieri, bensì apporta delle migliorie.
Nello specifico, il metodo degli indivisibili è un metodo prevalentemente geometrico per il calcolo di aree e volumi, può essere visto come una forma moderna del metodo di esaustione greco.
Un indivisibile, in termini moderni, può essere pensato come un ente geometrico di spessore infinitesimo, così ad esempio abbiamo che
- in \(\mathbb{R}^2\) un indivisibile è un segmento;
- in \(\mathbb{R}^3\) come indivisibili possiamo prendere sì dei segmenti, ma anche delle porzioni di piano (poiché si può dire che una porzione di piano è "di spessore infinitesimo" rispetto ad un volume).
Il metodo degli indivisibili consiste nel dividere la figura della quale si vuole calcolare l'area (o il volume) in opportuni indivisibili e poi "sommare" le loro lunghezze (o aree) così da ottenere la misura dell'area (o volume) della figura considerata.
A volte Wallis usa il metodo degli indivisibili in cui l'ha ricevuto da Cavalieri, altre volte invece lo amplia: per lui gli indivisibili non sono solamente segmenti in \(\mathbb{R}^2\) o aree in \(\mathbb{R}^3\), ma anche "aree di figure di altezza infinitesima" (o, come direbbe lui, "aree di figure alte \(\frac{1}{\infty}\)") in \(\mathbb{R}^2\) e "volumi di solidi di altezza infinitesima" in \(\mathbb{R}^3\) (in particolare, nel piano, Wallis è solito considerare dei parallelogrammi di altezza infinitesima come indivisibili).
Inoltre Wallis usa il metodo degli indivisibili per creare un processo che chiama "induzione", che non è però da intendersi nel senso moderno: la sua "induzione" è circa un passaggio al limite per step successivi, ma senza parlare esplicitamente di limite dato che non è un concetto appartenente alla sua epoca (bisognerà aspettare la pubblicazione del Cours d'analyse di Cauchy, nel 1821, per avere la prima buona definizione di limite).
Lo studio delle coniche nel De sectionibus conicis
L'intento di Wallis non è di far conoscere al lettore le coniche in ogni loro sfaccettatura, proprietà e applicazioni, per conoscere nel dettaglio tutte le proprietà delle coniche esistono già tanti altri trattati.
Il suo intento è di presentare le coniche in modo diverso ed innovativo, con un nuovo metodo rispetto a quanto è stato fatto finora.
La prima novità che si riscontra in questo trattato di Wallis è il fatto che, nonostante si parli di coniche (ovvero un argomento di geometria), affronta le dimostrazioni anche algebricamente invece che unicamente dal punto di vista geometrico. E' infatti convinto che le dimostrazioni algebriche siano valide tanto quanto quelle geometriche ed anzi spesso risultano più brevi, chiare ed universali.
La seconda riguarda il modo di considerare le coniche: il De sectionibus conicis è diviso in due parti, Pars prima e Pars secunda. Nella prima le coniche sono viste secondo la tradizione, ovvero come sezioni del cono. Nella seconda invece, ed è specialmente qui la grande novità, le coniche sono definite a partire da delle relazioni di carattere algebrico che le caratterizzano, ovvero sono viste come luogo dei punti.
E' proprio l'uso del metodo degli indivisibili che gli consente di fare questo passo poiché consente di esprimere il rapporto tra una sezione conica e la sua realizzazione nel piano.
Pars prima: le coniche viste come sezioni coniche
In questa prima parte del trattato le coniche sono definite "alla maniera di Apollonio", così la parabola risulta essere la sezione staccata su un cono (circolare e non necessariamente retto) da un piano parallelo ad una direttrice del cono.
La Pars prima è decisamente più breve della Pars secunda, contiene solamente 6 proposizioni riguardanti le coniche, due per ciascuna conica, che trattano della loro definizione come sezione conica e di come determinare il lato retto.
Le due proposizioni riguardanti la parabola nella Pars prima sono la VIII e la XII:
1) La proposizione VIII, intitolata "De parabola, sectione coni facta", afferma che
"I quadrati delle ordinate sono proporzionali alle parti di asse
comprese tra il punto d'intersezione delle ordinate ed il vertice."
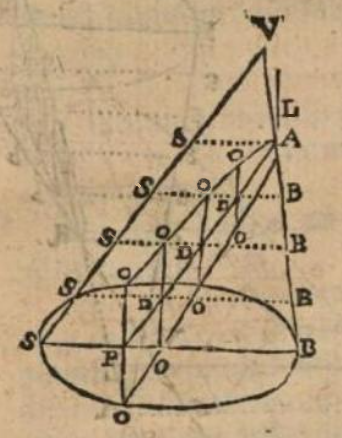
dove, guardando la figura, intende che \(DO^2\) e \(DA\) sono in proporzione [aritmetica].
Questa è una relazione già espressa nel mondo classico, ma viene qui letta nei termini del metodo degli indivisibili, usato per dimostrare la proposizione (si noti anche che questa relazione è la definizione odierna della parabola come luogo dei punti, cioè è l'equazione della parabola).
Nonostante non sia detto espressamente nell'enunciato, questa proposizione serve a Wallis anche per costruire la parabola. Infatti dopo aver dimostrato che \(DO^2\) e \(DA\) sono in proporzione aritmetica, Wallis conclude che "grazie al metodo degli indivisibili si può dire che l'intero piano della parabola è formato da un numero infinito di segmenti i cui quadrati sono in proporzione", ovvero sfrutta il metodo degli indivisibili per estendere la relazione appena dimostrata a tutti gli infiniti segmenti di asse ed alle infinite ordinate della parabola.
2) La proposizione XII, intitolata "De parabolae latere-recto", è divisa in due parti. Nella prima Wallis definisce il cosiddetto lato retto della parabola, mentre nella seconda dà un metodo per trovare il cono del quale la parabola è sezione (ricordiamo però che qui la parabola è ancora definita come sezione conica), passaggio importante ma già presente nella letteratura anteriore (ad esempio è presente già dal tempo di Apollonio).
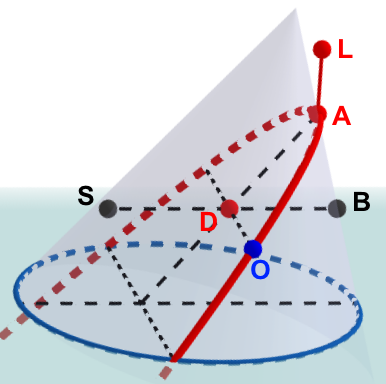Il lato retto \(LA\) è definito, sfruttando la proporzione vista nella proposizione VIII, come il quarto proporzionale tra \(DA\), \(BD\) e \(DS\), ovvero risulta essere il segmento tale che
\(DA\cdot LA=DO^2\)
L'importanza di questa dimostrazione risiede principalmente nel fatto che la relazione algebrica discendente da questa proposizione sarà poi usata nella Pars secunda per definire la parabola come luogo dei punti.
Pars secunda: le coniche viste come luoghi dei punti
In questa seconda parte del De sectionibus conicis, Wallis considera le proprietà delle coniche ottenute nella Pars prima come a sé stanti, ovvero qui definisce le coniche come curve piane, luoghi dei punti, astraendole dalla definizione come sezioni coniche. Così, come si diceva prima, la parabola è definita come quella curva piana che soddisfa la relazione della proposizione XII; più precisamente, la definizione di questa curva che Wallis chiama "parabola assoluta" è data nella proposizione XXI, intitolata "De parabola, absolute considerata":
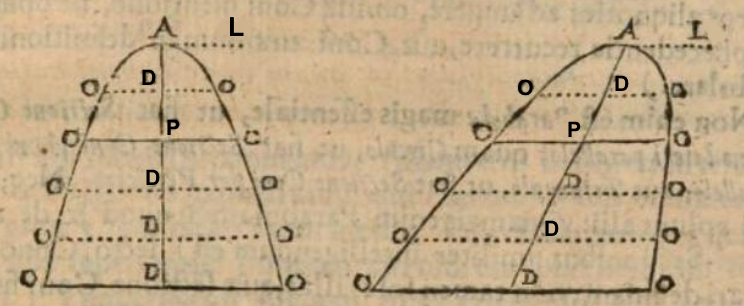
"Chiamo parabola la curva nella quale il quadrato delle ordinate è proporzionale al segmento di diametro
che congiunge il vertice con l'ordinata [...] e tale costante di proporzionalità la chiamo lato retto",
la parabola "assoluta" risulta allora definita proprio dall'equazione \(DO^2=DA\cdot AL\).
Questa proposizione è di importanza fondamentale poiché consente il passaggio dalla parabola vista come sezione del cono alla parabola vista sul piano come luogo dei punti (si ricordi che qui la parabola è definita analiticamente, come luogo dei punti). Tale passaggio è tutt'altro che banale e si può constatare che è stato trascurato in tutta la letteratura precedente e posteriore a Wallis.
Con questa proposizione (unita alla sua inversa), Wallis riesce in sostanza a dimostrare che le definizioni della parabola piana (come luogo dei punti) e della parabola "di Apollonio" (come sezione conica) sono del tutto equivalenti. Grazie a questa equivalenza si può affermare che ogni parabola piana ha il suo corrispettivo sul cono (e viceversa).
Per di più non serve dimostrare che le stesse proprietà valgono sia per la parabola sul piano che per quella sul cono poiché l'equivalenza assicura che dimostrando una proprietà per una parabola piana, tale proprietà vale anche per la parabola come sezione conica (e viceversa).
Per dimostrare la proposizione, Wallis costruisce esplicitamente il cono del quale la parabola piana è sezione, è dunque una dimostrazione costruttiva (si veda il testo completo, pagine 30-34, per maggiori dettagli). Al seguente link è presente una costruzione già pronta: https://www.geogebra.org/m/cu2j49tu.
Wallis esplicita anche per l'ellisse e l'iperbole "assolute", ovvero come curve piane, una costruzione del cono di cui sono sezione analoga a quanto visto per la parabola; queste due costruzioni sono contenute rispettivamente nella proposizione XXVI e proposizione XXXIII.
Calcolo dell'area dei segmenti parabolici
Il calcolo dell'area di un segmento parabolico (detto anche "quadratura della parabola") è contenuto nell'opera Arithmetica infinitorum, non nel De sectionibus conicis. Ciò accade probabilmente poiché questo argomento era più visto da Wallis come relativo al calcolo o all'algebra che alla geometria.
Wallis calcola l'area del segmento parabolico \(ADO\) come in figura
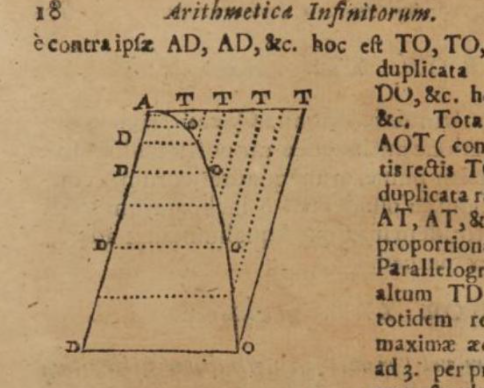Per farlo, sfrutta il metodo degli indivisibili per attuare una sorta di passaggio al limite e giunge alla conclusione che tale area è \(\dfrac{1}{3}\) dell'area del parallelogrammo \(ADOT\) nel quale il segmento parabolico è "inscritto". In ultimo aggiungiamo soltanto che Wallis ricevette molte critiche per questi "passaggi al limite" presenti nelle sue opere, infatti non si può parlare propriamente di concetto di limite dal momento che bisognerà aspettare l'opera di Cauchy del 1821 per avere una prima buona definizione di limite, di conseguenza all'epoca di Wallis questi procedimenti erano poco rigorosi.