

Newton naque a Woolsthorpe-by-Colsterworth, vicino a Grantham, da una famiglia di allevatori, il 4 gennaio 1643. Suo padre morì tre mesi prima della sua nascita, mentre sua madre, Hannah Ayscough, si risposò circa tre anni dopo con Barnabas Smith, un agiato chierico.
Con la morte del patrigno, avvenuta nel 1653, Newton ricevette una consistente eredità che gli permise di frequentare la scuola pubblica di Grantham. Alla fine del 1658, Newton fu costretto dalla madre ad abbandonare gli studi per gestire il patrimonio familiare, ma il maestro Stokes convinse la madre a lasciargli proseguire gli studi. Fu così che Isaac, nel 1661, si trasferì a Cambridge, con lo scopo di ottenere una laurea in legge al Trinity College.
Successivamente, quando nel 1665 il Trinity College venne chiuso a causa della peste, egli ne approfittò per proseguire gli studi autonomamente, ottenendo i suoi primi grandi risultati di carattere matematico. Tra questi ricordiamo la formula binomiale per un esponente razionale qualunque, il metodo generale per costruire le tangente alle curve, che lui chiama metodo delle flussioni, ed il Metodo di Newton per approssimare le radici di un'equazione.
Nel 1667 il Trinity College riaprì e l'anno successivo Newton consegnò al suo professore Barrow il De analysi per aequationes numero terminorum infinitas, nel quale esponeva le sue idee riguardo alla matematica dell'Infinito. Fu questo trattato, reputato grandioso anche da John Collins (1625-1683), ad indurre Barrow a lasciare la cattedra per permettere a Newton di prendere il suo posto.
Pertanto, l'8 novembre 1669, Newton divenne professore lucasiano ed iniziò così il suo periodo più produttivo. Dal 1670 al 1672 si occupò di ottica, mentre nel 1679 riprese lo studio delle sue idee sulla gravità, sulla meccanica classica e sulle leggi di Keplero. Queste sue scoperte verranno poi inserite all'interno dei Philosophiae Naturalis Principia Mathematica, opera prodotta e pubblicata su convincimento di Edmund Halley nel 1687.
Infine, nel 1696 Newton si trasferì a Londra per accettare un incarico, offertogli da Charles Montagu, I duca di Manchester, alla zecca reale, diventandone poi direttore nell'anno successivo. Egli morì a Kensington, Londra, all'età di 84 anni, il 31 marzo 1727 e fu sepolto otto giorni dopo nell'Abbazia di Westminster.
L'opera, nota anche con l'abbreviazione De Analysi, scritta nel 1669 e pubblicata nel 1711, è un piccolo trattato in cui Newton sistematizza i suoi risultati sulla risoluzione dei problemi di quadratura per mezzo di serie infinite.
Nel libro, completato nel 1671, ma pubblicato nel 1742 (sebbene ne fosse apparsa una traduzione inglese nel 1736), Newton illustra il suo Metodo delle Flussioni e ottiene semplici metodi analitici per risolvere problemi riguardanti le aree, le tangenti e la lunghezza delle curve.
Considerata un capolavoro assoluto della storia della scienza, l'opera è nata dall'ampliamento di un manoscritto inviato a Edmond Halley nel novembre del 1684, intitolato De motu corporum in gyrum, nel quale Newton forniva importanti deduzioni matematiche relative alle tre relazioni oggi conosciute come Leggi di Keplero. Su incoraggiamento di Halley, Newton ha così continuato a sviluppare i Principia a partire dai concetti contenuti nel De motu.
L'opera, pubblicata nel luglio del 1687, consiste di tre libri: il primo, dal titolo
De motu corporum (Sul movimento dei corpi), è un'esposizione delle
definizioni di base sulla dinamica, dei tre principi della dinamica e delle conseguenti
deduzioni basate su di queste; il secondo, intitolato come il precedente, tratta
dell'idrodinamica e dell'idrostatica; il terzo, De mundi systemate (Sul
sistema del mondo), è invece un saggio sulla gravitazione universale nel quale
vengono anche applicate le leggi stabilite nei libri precedenti al sistema solare e
alle comete. 
L'opera, pubblicata nel 1704, analizza la natura fondamentale della luce mediante la rifrazione attraverso prismi e lenti, i fenomeni di diffrazione e di scomposizione della luce nello spettro dei suoi colori componenti. Questo è suddiviso in tre libri e costituisce la seconda opera più importante di Newton. Nell'edizione del 1704 è presente, in appendice, il Tractatus de quadratura curvarum, ossia un trattato sulla quadratura delle curve.
Il testo, scritto in latino, è stato curato e pubblicato nel 1707 da William Whiston, il successore di Newton come professore lucasiano di Matematica presso l'Università di Cambridge, ed è basato sugli appunti delle lezioni tenute da Newton. Esso tratta infatti di aritmetica, di notazioni algebriche, della relazione tra geometria e algebra e di soluzioni di equazioni, applicando la regola dei segni di Cartesio a radici immaginarie.
Newton, diversamente da Apollonio, non scrisse mai un'opera avente come argomento centrale le sezioni coniche, ma inserì i suoi risultati all'interno dei Philosophiae Naturalis Principia Mathematica. Secondo Guicciardini, possiamo trovare le prime tracce della ricerca di Newton sul problema di Pappo nei suoi due manoscritti Veterum Loca Solida Restituta e Solutio Problematis Veterum de Loco Solido, prodotti nel periodo 1670-1680. è proprio questo secondo manoscritto ad essere stato incluso nel primo libro dei Principia, diventandone così la sezione V, intitolata Inventio orbium ubi umbilicus neuter datur (Come si trovano le orbite quando non è dato alcun fuoco). Inoltre, in questa sezione, oltre alla soluzione al problema di Pappo per le quattro rette (Lemmi 18 e 19), Newton dimostra anche la costruzione organica delle sezioni coniche (Lemma 21) e determina la conica passante per 5-n punti e tangente a n rette in posizione data, con n=0,1,...,5 (Prop. 22-27).
Per dimostrare i suoi risultati, Newton ricorre alle Proposizioni 17 e 18 del terzo libro delle Coniche di Apollonio, le quali equivalgono al cosiddetto "teorema delle corde intersecanti", o brevemente "teorema delle corde", per le sezioni coniche, che qui riportiamo.
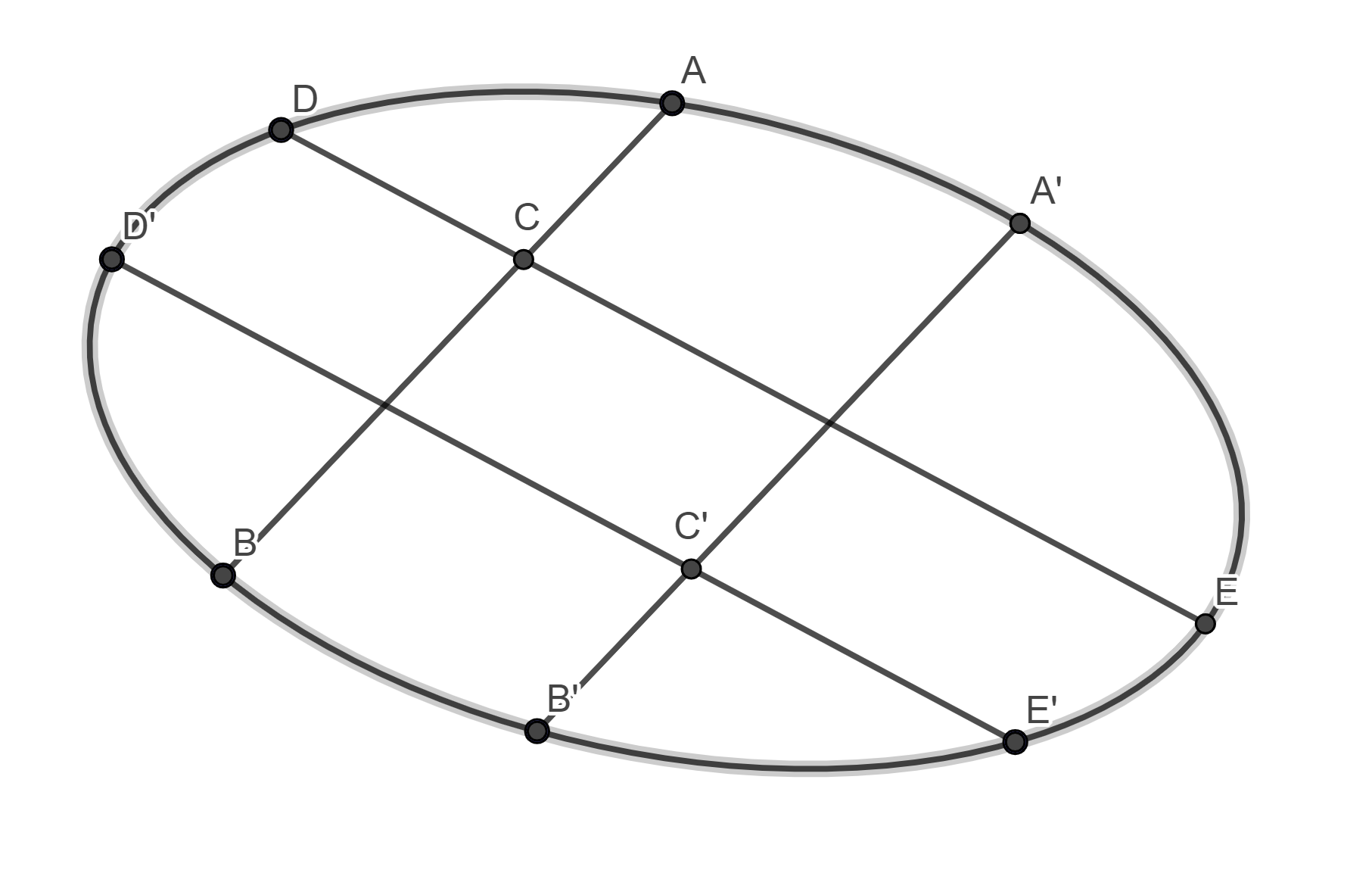
Teorema delle Corde. Data una sezione conica, se si considerano le due coppie di corde parallale AB, A′B′ e DE, D′E′, allora vale la seguente relazione
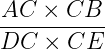 = = 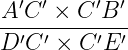 . .
|
Per completezza, riportiamo anche l'enunciato del problema di Pappo.
Problema di Pappo. Date 2n rette, trovare il luogo dei punti tali che il prodotto delle distanze dalle prime n rette sia uguale al prodotto delle distanze dalle rimanenti.
In questa sezione illustriamo come il problema di Pappo è stato risolto da Newton, il cui approccio può essere suddiviso in due parti:
Si può inoltre osservare che Newton ha affrontato lo studio del problema di Pappo perché gli si è presentato naturalmente sulla via della determinazione delle orbite.
Lemma 17. Sia dato un quadrilatero qualunque ABCD, inscritto in una data sezione conica, del quale sono stati prolungati infinitamente i quattro lati AB, CD, AC e DB. Se da un punto P qualsiasi di tale sezione conica si conducono sui quattro lati del quadrilatero altrettante rette PQ, PR, PS e PT, secondo angoli assegnati, ciascuna retta su ciascun lato, allora il rettangolo PQ × PR starà al rettangolo PS × PT in un rapporto dato costante.
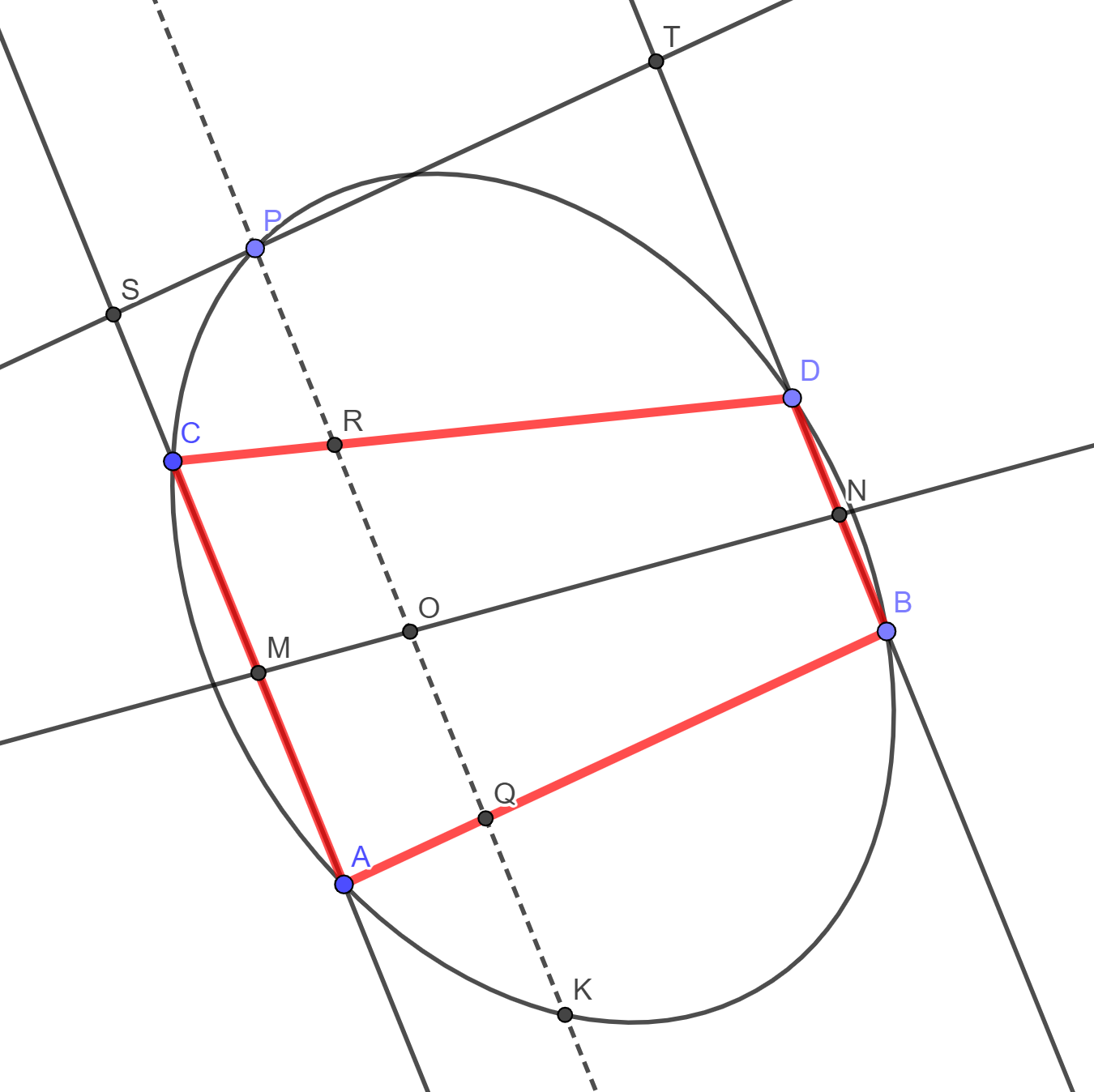
Newton dimostra poi, con il Lemma 18, che vale anche il viceversa di questo Lemma 17.
Lemma 19. Si trovi un punto P tale che, se a partire da esso vengono condotte, secondo angoli assegnati, quattro rette PQ, PR, PS, PT su altrettante rette di posizione data AB, CD, AC e BD, ciascuna delle prime su ciascuna delle seconde, il rettangolo PQ × PR sta al rettangolo PS × PT in un rapporto dato costante.
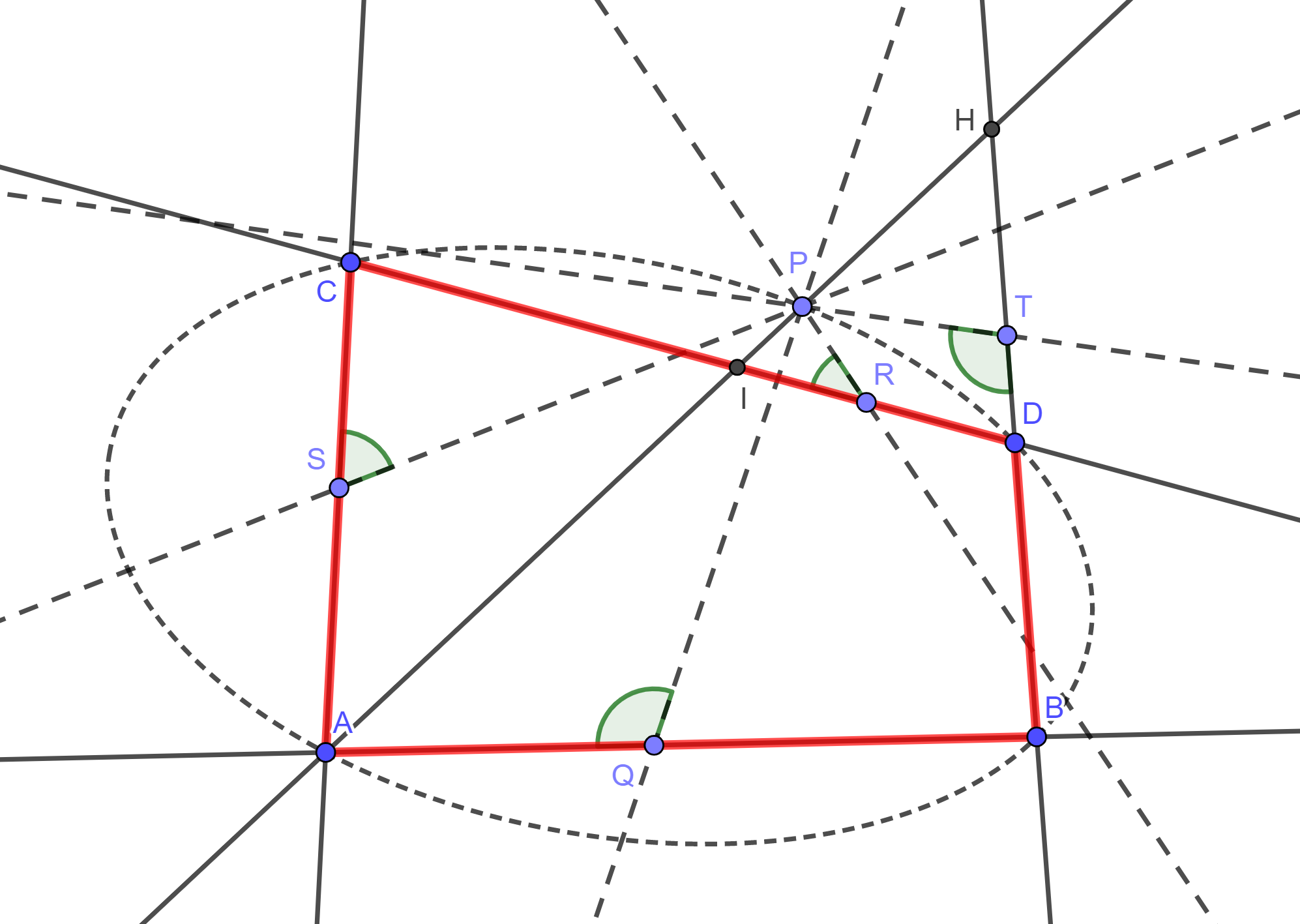
Successivamente seguono due Corollari: nel primo Newton mostra come determinare la tangente alla conica in un punto qualunque, mentre nel secondo spiega come trovare il diametro e il relativo parametro che definisce la natura della sezione conica data dagli infiniti punti P trovati attraverso il Lemma 19.
è con questo secondo Corollario al Lemma 19 che si conclude la prima parte della soluzione geometrica al problema di Pappo delle quattro rette.
Lemma 20. Si consideri un parallelogramma qualunque ASPQ tale per cui i vertici opposti A e P giacciono su una sezione conica. Si suppone inoltre che le rette su cui giacciono i due lati AQ e AS intersechino tale sezione conica nei punti B e C rispettivamente. Se da un qualsiasi punto D appartenente alla conica, distinto dai precedenti, si tracciano le rette BD e CD che incontrano gli altri due lati del parallelogramma PS e PQ rispettivamente in T e in R, allora i segmenti PR e PT saranno in un dato rapporto. Viceversa, se PR e PT sono in un dato rapporto, allora il punto D giacerà sulla sezione conica passante per i punti A, B, C, P.
A questo Lemma seguono poi tre Corollari: nel terzo, in particolare, Newton dimostra che due sezioni coniche distinte non possono intersecarsi in più di quattro punti. Pertanto, si può concludere che per cinque punti distinti passa una e una sola conica.
è dunque ora possibile ottenere la costruzione organica per le sezioni coniche.
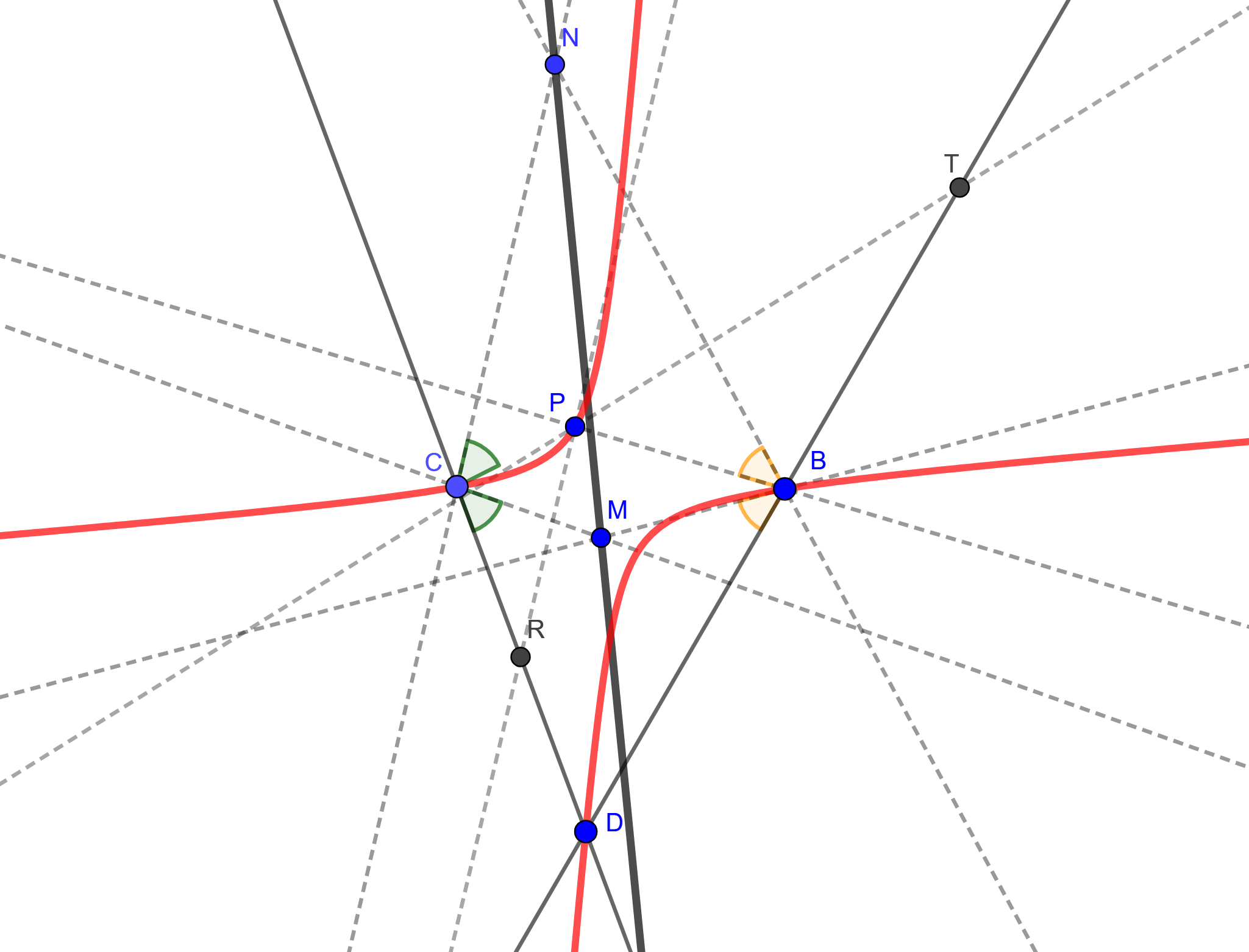
Lemma 21 - Costruzione Organica. Dati due punti M e N e due poli B e C, si considerino le rette BM e CM, passanti per M e rotanti attorno ai poli, e la retta MN. Si traccino poi due rette BD e CD in modo tale che formino angoli fissati, DBM e DCM, con BM e CM. Muovendo il punto M lungo la retta MN, mantenendo gli angoli fissati, si ha che il punto D descrive una sezione conica passante per B e C.
Viceversa, dati tre punti fissi A, B, C sulla conica, e un punto D mobile, sempre sulla conica, se l'angolo DBM è sempre uguale all'angolo dato ABC e l'angolo DCM è sempre uguale all'angolo dato ACB, allora il punto M starà su una retta di posizione data.
Successivamente, con la Proposizione 22, Newton dimostra come ottenere la sezione conica passante per cinque punti qualunque, nella prima fa uso del Lemma 20, mentre nella seconda richiama il Lemma 21, ossia la costruzione organica. A questa seguono poi altre Proposizioni (23-27), nelle quali egli ha determinato la sezione conica passante per 5 - n punti e tangente a n rette in posizione data, con n = 1,..., 5.
D'altra parte, nel manoscritto Veterum loca solida restituta, egli determina la conica passante per cinque punti utilizzando direttamente il teorema delle corde: egli descrive prima la conica passante per tre punti e dato il suo centro, poi, dati i cinque punti, determina il centro della conica e utilizza quanto ottenuto in precedenza.