IL PASSAGGIO DAL CONO AL PIANO
LE SEZIONI CONICHE COME CURVE PIANE PER CLAUDE MYDORGE
(a cura di Monica Mancini)
Viene qui presentato il contributo allo sviluppo della teoria delle sezioni coniche del matematico francese Claude Mydorge (1585-1647).
Sebbene la figura di Mydorge sia poco nota perché non ha ricevuto molta attenzione nella letteratura corrente, egli era stimato come un savant (sapiente) nella Parigi del XVII secolo, tanto che Descartes lo ritenne uno dei più grandi matematici del suo tempo.
Claude Mydorge (1585-1647) nacque, visse e mor&iigrave; a Parigi in una delle più illustri e ricche famiglie di Francia. Studiò presso il Collegio dei Gesuiti di La Flèche e successivamente si formò come avvocato, prima di intraprendere una carriera legale e amministrativa. Dopo aver prestato servizio come conseiller (consigliere) alla corte del Grand Châtelet (palazzo di giustizia e sede della polizia), divenne tesoriere della Généralité di Amiens (generale delle finanze a guida del distretto finanziario della città di Amiens).
L'impiego scelto da Mydorge gli concesse tempo sufficiente per coniugare il lavoro previsto dal suo incarico pubblico con la vita di un savant (sapiente). La sua posizione lavorativa era ideale per due motivi: il primo é che era una posizione di grande rilevanza e solo una figura di alto rango, come Mydorge vista la sua famiglia, poteva occupare tale posizione; in secondo luogo, consisteva in compiti e mansioni leggere, il che significava poter dedicare molto tempo alla materia che più lo appassionava, la matematica, e ad altre discipline ad essa connesse, come l'astronomia e l'ottica.
Nel 1625 Mydorge incontrò R. Descartes (1596-1650) a Parigi. Si instaurò velocemente una solida relazione tra i due che durò per il resto della loro vita. Come attesta il principale biografo di Descartes, Baillet, Mydorge era considerato un "amico prudente e fedele" ed era da lui ritenuto il "primo matematico di Francia del suo tempo".
Mydorge apparteneva al Circolo di Mersenne a Parigi, all'interno del quale godeva di grande stima: questo Circolo raccoglieva presso il Collegio dei Frati Minori le personalità più evolute culturalmente attorno alla figura di Padre Marin Mersenne, un teologo, filosofo e matematico francese che ag&iigrave; come veicolo per la circolazione di informazioni e scoperte scientifiche in un'epoca in cui i journals (riviste scientifiche) non esistevano ancora. Nel Circolo convergevano i savants e gli amateurs de science del tempo: i primi, i "sapienti", erano coloro che erano ritenuti capaci di esprimere ed elaborare le proprie idee; i secondi, gli "amanti della scienza", erano coloro che erano in grado di capire e far proprie tali idee.
Sebbene fosse una figura ben conosciuta nella Parigi culturale e scientifica del 1625-1645, poche informazioni su Mydorge sono state trasmesse alle generazioni a lui successive.
Lo studio dei sistemi ottici portò Mydorge all'analisi approfondita delle sezioni coniche.
Tra il 1640 e il 1647, anno della sua morte, Mydorge divenne meno produttivo e la sua figura fu accompagnata da una "reputazione di grande integrità di vita".
L'opera principale di Claude Mydorge sulle sezioni coniche è il trattato Prodromi catoptricorum et dioptricorum sive Conicorum operis ad abdita radii reflexi et refracti mysteria praevij et facem praeferentis. Libri quatour priores (1639). Questo lavoro, insieme ad alcuni altri scritti sulle coniche dei suoi contemporanei (Descartes, Fermat, Desargues e Pascal) era condiviso e letto soprattutto all'interno del Circolo fondato da Marin Marsenne.
Il titolo propone questa raccolta di libri come un prerequisito essenziale per lo studio dei fenomeni di rifrazione e di riflessione. Nel progetto di Mydorge vi erano altri quattro libri (preparati dall'autore e perduti dopo la sua morte) nei quali avremmo potuto leggere come, usando le coniche, tali fenomeni fisici potessero essere affrontati.
Per una descrizione più dettagliata dell'opera consultare la versione completa del documento.
Lo scopo dell'opera è duplice: documentare e raccogliere la "dottrina" sulle coniche e allo stesso tempo scrivere un trattato utile per chi voleva risolvere problemi di ottica, in particolare relativi a sistemi catottrici (costituiti unicamente da superfici riflettenti come gli specchi) e diottrici (costituiti unicamente da elementi rifrangenti come le lenti).
Il tentativo di Mydorge fu quello di dare al lettore una solida base di conoscenze essenziali sulle sezioni coniche, prima di affrontare i problemi legati ai fenomeni naturali. Sappiamo che per la stesura di questa prima parte teorica Mydorge consultò gli Elementi conici di Apollonio nell'edizione del 1566 di Commandino (questo nome, infatti, compare diverse volte nei libri III e IV del Prodromi). Ma a differenza di Apollonio, l'obiettivo di Mydorge non è quello di presentare una teoria delle coniche pura e astratta, ma quello di insegnare a costruire le coniche perché necessarie per risolvere problemi, in particolare problemi di fisica. E forse proprio davanti alle difficoltà poste da qualche specifico problema di costruzione di qualche specchio o lente Mydorge si rese conto che non è importante tanto il fatto che la conica che viene utilizzata sia sezione di qualche cono quanto il fatto di essere in grado di tracciare la conica su un foglio di carta, per poi tracciarla su un materiale più resistente ed infine considerare il solido di rotazione che da essa si può ottenere. Cos&iigrave; facendo si potrà costruire uno specifico specchio o una particolare lente.
Prodromi catoptricorum et dioptricorum può essere considerato uno dei primi momenti della geometria in cui l'attenzione sulle coniche è focalizzata sulla loro costruzione in quanto curve in un piano. Passando dal primo al secondo libro del suo trattato, viene sottolineato il fatto che le proprietà delle coniche come sezioni di un cono sono le stesse quando vengono considerate come curve piane, aprendo cos&iigrave; la strada alla trattazione delle coniche all'interno della geometria analitica.
In conclusione, l'obiettivo di Mydorge era quello di creare un'edizione di un trattato sulle coniche, avendo il testo di Apollonio come punto di riferimento, che fosse alla portata degli amanti di ottica, i quali avrebbero utilizzato l'opera come un manuale operativo ma anche arricchente per i lettori che desiderassero raggiungere una conoscenza approfondita sull'argomento.
è sicuramente utile conoscere quel fosse lo "stato dell'arte" sulle coniche nel periodo immediatamente precedente e contemporaneo alla pubblicazione del trattato di Mydorge.
Alla fine del XVI secolo possono essere individuate tre linee attraverso le quali le conoscenze sulle coniche venivano tramandate:
1. la prima è rappresentata dalla trasmissione degli Elementi conici di Apollonio nell'Occidente;
2. la seconda è la presenza di trattati sugli specchi ustori e sulla prospettiva;
3. la terza riguarda l'applicazione delle sezioni coniche nella determinazione delle linee d'ombra delle meridiane (o orologi solari).
Questo acceso interesse verso una maggiore comprensione ed applicazione delle sezioni coniche della fine del XVI secolo è indispensabile
per capire perché e in che modo diversi matematici si orientarono allo studio delle coniche nei primi 60 anni del secolo successivo.
In questi anni, infatti, furono pubblicati diversi trattati inerenti le coniche: ricordiamo, fra tanti, Lo specchio ustorio di Bonaventura Cavalieri (1632), l'opera di René Descartes Géométrie (1637) che per la prima volta identifica le coniche tramite equazioni specifiche e ancora il Traité (1639) di Gerard Desargues nel quale le coniche sono applicate per risolvere problemi di prospettiva nella pittura.
Successivamente alla pubblicazione dei volumi di Mydorge, la produzione di manuali che trattano le coniche e le loro possibili applicazioni per risolvere problemi di vario tipo prosegu&iigrave;: nel 1644 padre Marin Mersenne pubblicò Universae géométrie a Parigi, opera all'interno della quale sono raccolti scritti sulle coniche di autori antichi e recenti (tra i quali Mydorge stesso) volti allo studio dei fenomeni di rifrazione; nel 1655 John Wallis diede alle stampe il suo De sectionibus conicis nel quale mostrò l'importante risultato del passaggio dalle coniche come curve nel piano alle coniche come sezioni di un cono.
Questo breve excursus sugli scritti dei primi sessant'anni del XVII secolo denota come gli Elementi conici di Apollonio, pur rimanendo un sicuro punto di riferimento culturale, non era più sufficiente per rispondere alle esigenze dei matematici del tempo. Vi era l'esigenza di studiare queste curve per risolvere problemi di fisica, astronomia ed altri campi della scienza.
A cominciare dai primi decenni del 1600 le coniche erano viste come luoghi di punti, ovvero curve nel piano e non più come sezioni di un cono. Mydorge ricopr&iigrave; un ruolo fondamentale in questo passaggio concettuale nella storia delle coniche. Questo può essere considerato uno dei primi momenti in cui l'attenzione sulle coniche viene centrata sulla loro costruzione come curve piane.
Nel secondo libro del trattato di Mydorge si trovano una serie di problemi risolti per costruire le sezioni coniche per punti. Di seguito è riportato il problema, il protocollo di costruzione ideato da Mydorge e l'immagine ricostruita grazie al software di geometria dinamica GeoGebra per la parabola.
Per le costruzioni delle altre sezioni coniche e per l'insieme completo delle proposizioni che giustificano tali costruzioni consultare la versione completa del documento.
Per tracciare ogni sezione conica, trovato un certo numero di punti ripetendo a piacere il protocollo di costruzione, rimane il problema di come unire tali punti per ottenere la conica. Mydorge scrisse «aeliquabili manu ducta» nel proprio trattato, ovvero congiungere i punti «con mano ferma e che compie un'azione continua».
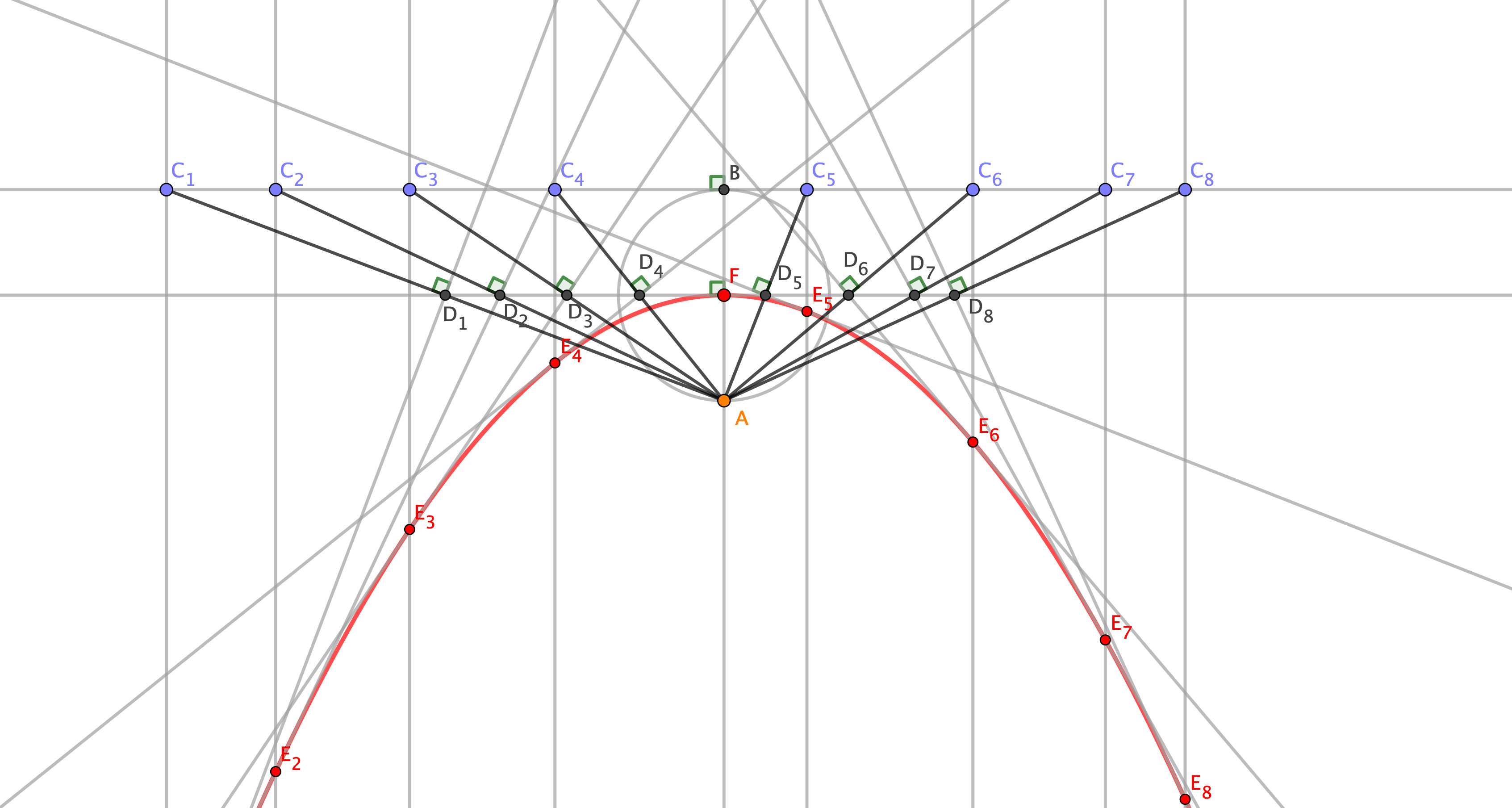
Libro II, Problema 1 - Costruzione della parabola per punti
Dati per posizione il fuoco ed il vertice di una parabola, descrivere nello stesso piano la parabola per punti.
Protocollo di costruzione
Siano $A$ il fuoco e $F$ il vertice di una parabola.
Tracciamo $AF$ e prolunghiamola fino al punto $B$ in modo che sia $AF = FB$.
Dal punto $F$ tracciamo $FD$ perpendicolare ad $AB$ e prolunghiamola quanto vogliamo.
Dal punto $B$ tracciamo $BC$ perpendicolare ad $AB$ e prolunghiamola quanto vogliamo.
Scegliamo su $BC$ quanti punti vogliamo $C_i$.
Uniamo ogni $C_i$ con $A$.
Ogni retta $AC_i$ interseca $FD$ nei punti $D_i$.
Dai punti $C_i$ tracciamo le parallele ad $AB$.
Dai punti $D_i$ tracciamo le perpendicolari alle rette $AC_i$. Tali perpendicolari intersecano le parallele ad $AB$, tracciate dai punti $C_i$, nei punti $E_i$.
Per la prima proposizione preliminare, i punti $E_i$ si trovano su una stessa parabola di vertice $F$ e fuoco $A$. Se questi punti sono congiunti con una curva «aequabili manu ducta», questa curva è una parabola.
Il file con la costruzione è scaricabile qui.
Mydorge va anche ricordato per aver riacceso l'interesse verso il cosiddetto Teorema delle corde. Nel 1639, all'interno del quarto libro del Prodromi catoptricurum et dioptricorum, Mydorge dimostrò il teorema delle corde e lo utilizzò per disegnare per punti la sezione conica passante per cinque punti dati sullo stesso piano.
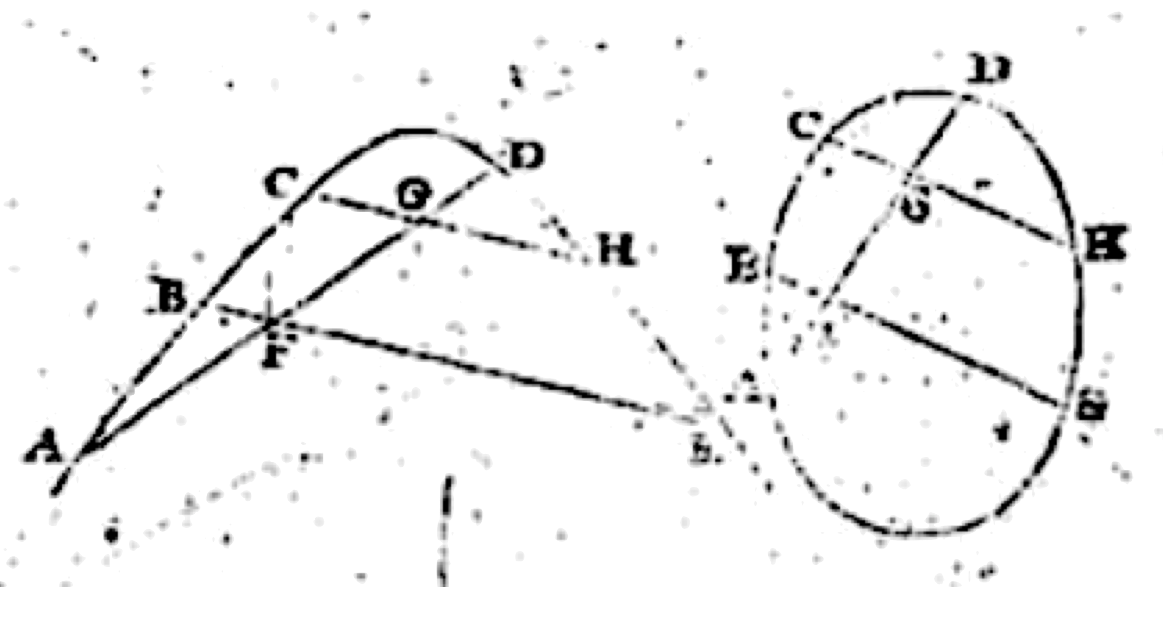
Libro IV, Proposizione 27 - Teorema delle corde
Se in una sezione conica, o in una circonferenza, si disegnano due rette parallele che intersecano un'altra retta secante la conica, i rettangoli costruiti con i segmenti delle corde parallele stanno tra loro come i rettangoli costruiti con i segmenti ottenuti sulla terza corda secante.
$AHC : DIE = FHG : FIG$
In modo simile ad Apollonio, anche Mydorge presentò la dimostrazione del teorema delle corde molto avanti nella sua opera (libro IV): questo perché fece ampio utilizzo di proprietà delle coniche presentate nei libri precedenti.
Ma diversamente da Apollonio, Mydorge utilizzò il teorema delle corde per risolvere problemi inerenti le coniche, in particolare il problema posto da Pappo (e da lui risolto solo parzialmente) del determinare una sezione conica dati cinque punti. Mydorge ottenne l'importante risultato di risolvere il problema per tutte le sezioni coniche.
Per la dimostrazione del teorema delle corde di Mydorge consultare la versione completa del documento.
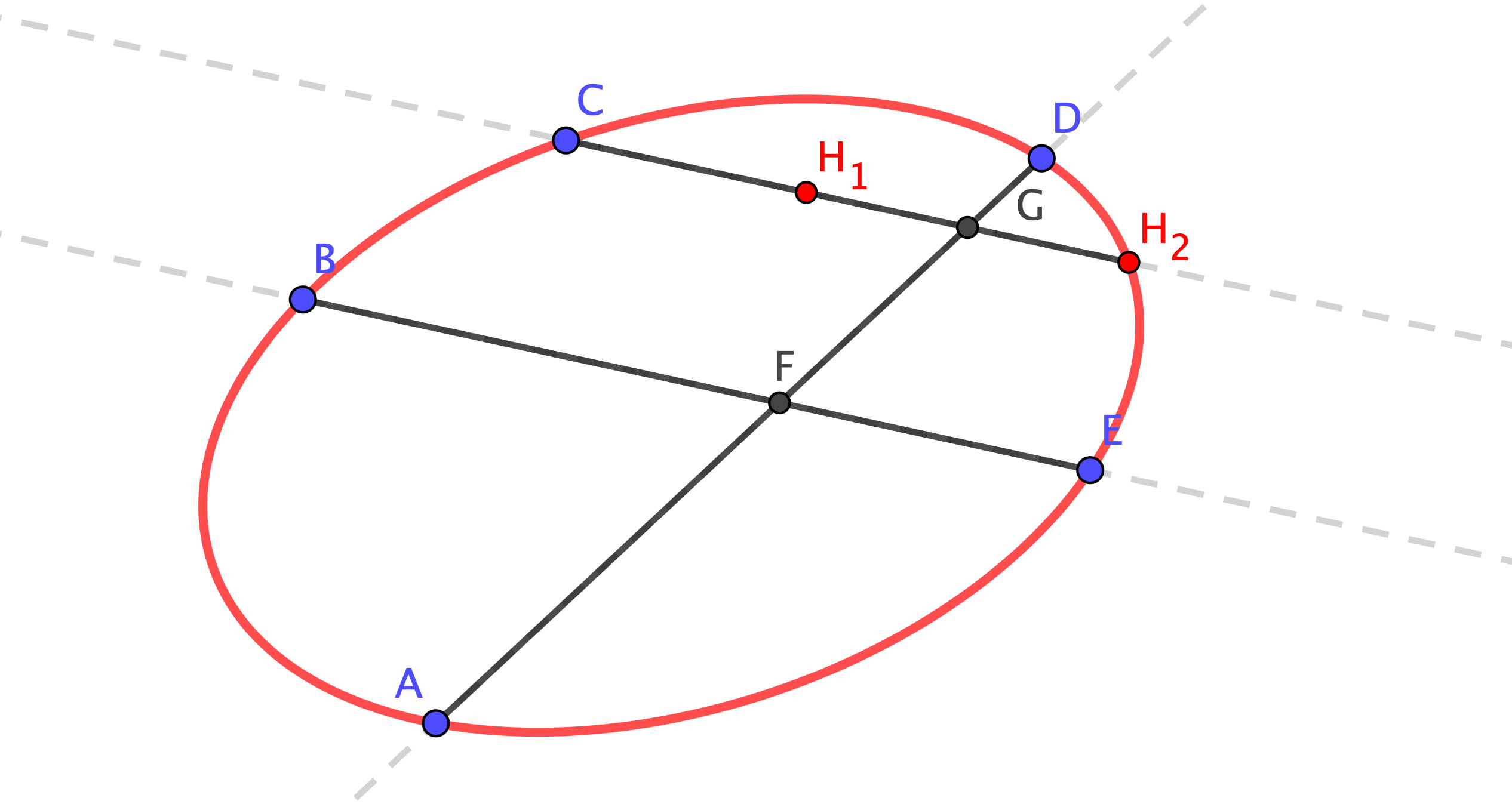
Libro IV, Proposizione 34 - Conica per cinque punti
Dati cinque punti su uno stesso piano, disegnare per punti la sezione conica passante per essi.
Protocollo di costruzione
Chiamiamo $F$ il punto di intersezione delle due rette $AD$ e $BE$.
Tracciare la retta $CG$ parallela a $BE$, estendendola in modo tale che il punto $H$ che giace su di essa sia tale che $(CG \cdot GH) : (AG \cdot GD) = (BF \cdot FE) : (AF \cdot FD)$.
Per il teorema delle corde possiamo affermare che $H$ appartiene alla sezione conica passante per $A$, $B$, $C$, $D$, $E$ (al tempo era già noto che per cinque punti passa una e una sola sezione conica).
Il file con la costruzione è scaricabile qui.
