

Philippe de La Hire
, geometra, geodeta, matematico e astronomo nato a Parigi il 18 marzo 1640, morto ivi il 21 aprile 1718. Figlio del pittore Laurent de La Hire, abbandonò l'arte, cui si era dapprima indirizzato, per darsi alla scienza.
Il padre Laurent, divenuto pittore di una certa fama a Parigi, con la moglie Marguerite Coquin, fece della loro casa un luogo stimolante dove crescere dei figli: essi avevano infatti l'abitudine di intrattenere nella loro casa scienziati, artisti e matematici, il più rilevante dei quali era Girard Desargues (1591-1661).
Philippe fu educato come artista e divenne abile in disegno e pittura e non ricevette nessuna istruzione formale, né scolastica né universitaria. Il padre si aspettava che seguisse la sua stessa professione e lo istruì di conseguenza. Nel 1660, all'età di diciassette anni, perse il padre e partì per l'Italia e trascorse quattro anni a Venezia sviluppando le sue capacità artistiche e la geometria. Fu proprio quest'ultima ad accendere la fiamma di quella che si rivelò poi la sua vera passione: la matematica. Egli infatti, nonostante apprese la geometria per imparare la prospettiva nell'arte, trovava molto più piacevoli le lezioni di matematica che non quelle di pittura.
Dopo il suo ritorno dall'Italia Philippe continuò a dipingere, ma i suoi studi rimasero devoti alla geometria. Egli inoltre avevo un amico, Abraham Bosse, col quale condivideva entrambe le passioni: arte e matematica. Anche Bosse frequentò i corsi di geometria di Girard Desargues dal 1641. Desargues, che La Hire conobbe fin dall'infanzia grazie ai genitori, morì nel 1661 e nello stesso anno Bosse fondò la sua scuola di arte. A questo punto, influenzato dai lavori di Desargues, sia direttamente sia indirettamente grazie a una serie di lavori pubblicati dall'amico Bosse sulla geometria imparata da Desargues stesso, La Hire iniziò a studiare le sezioni coniche, che trattò dal punto di vista proiettivo.
Il 26 gennaio 1678 fu eletto alla Académie des Sciences nella sezione di astronomia.
La produzione di La Hire conta fondamentalmente quattordici opere che spaziano tra geometria, astronomia, meccanica e architettura, tanto per citare alcuni argomenti. Di particolare interesse per questo studio sono le opere riguardanti la trattazione delle sezioni coniche:

Tutte le costruzioni e le dimostrazioni di La Hire si basano sulla divisione armonica di un segmento. Il problema dell'arco rampante consiste nel trovare l'arco di una conica tangente a due rette date in due punti assegnati, e tangente inoltre ad una terza retta. Il punto chiave si trova nella proposizione IV, che in termini moderni può essere così descritta:
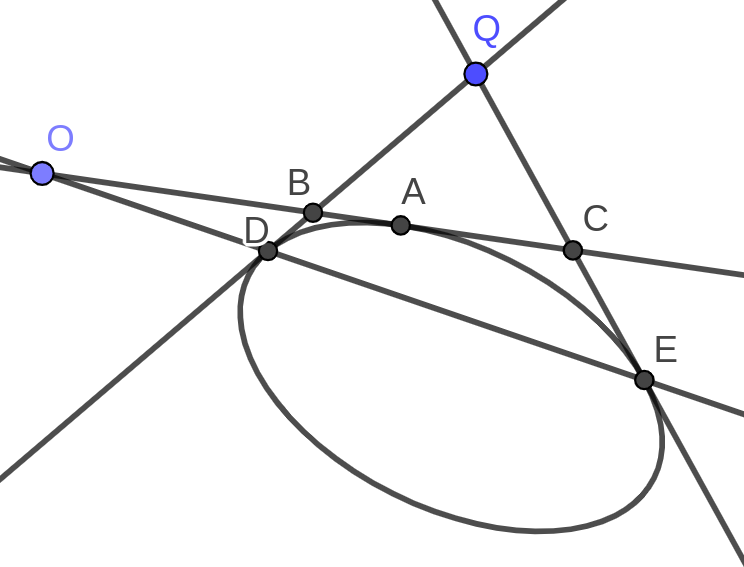
siano date tre rette tangenti ad una sezione conica BC, BD e CE (figura 3).
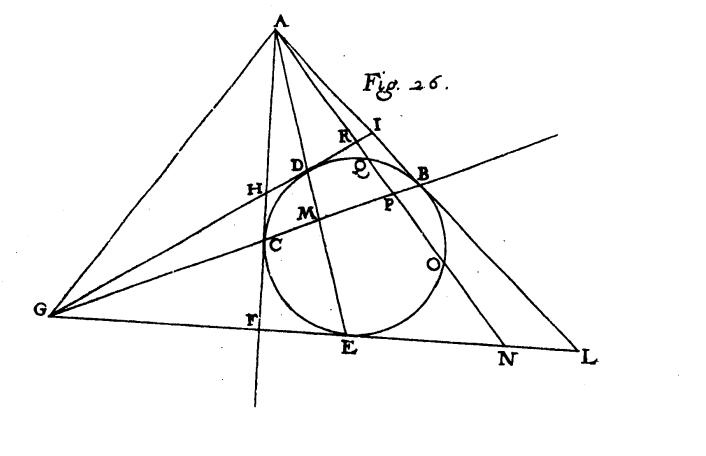
Si supponga che le tangenti DB ed EC, tangenti alla conica rispettivamente in D ed E, si intersechino in Q, e che la retta DE intersechi la tangente BC in O. Allora, essendo A il punto di tangenza di BC, si ha che \( \frac{OB}{OC}=\frac{BA}{CA}\), ossia A è il quarto armonico dopo B, C e O.
Pertanto, conoscendo i punti di tangenza della seconda e della terza retta, La Hire poteva trovare anche il punto di tangenza della prima.
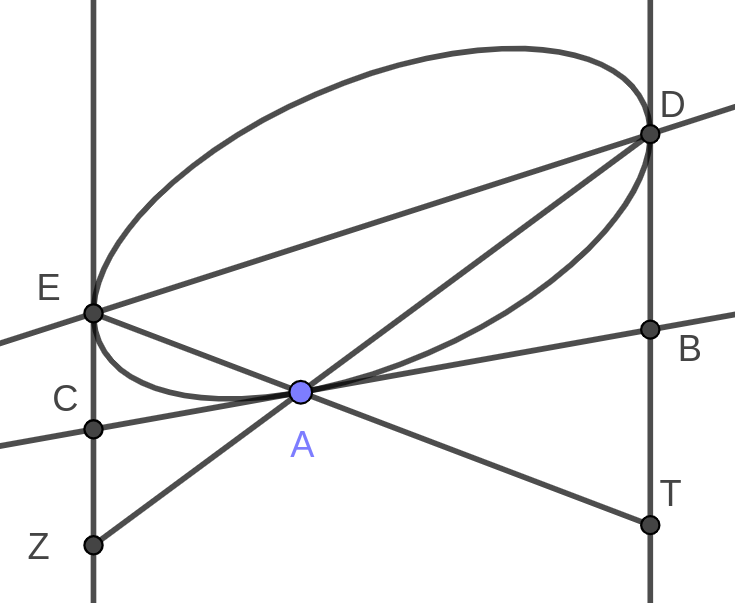
Nella proposizione III egli considerò il caso particolare in cui le tangenti DB ed EC sono parallele, poiché non considerò mai i punti all'infinito (figura 2): in questo caso La Hire dimostra che la sezione conica è necessariamente una circonferenza, o un'ellisse, e che la retta ED che unisce i punti di tangenza è un diametro.
Applicando le proposizioni 29 e 30 e il viceversa della proposizione 27 del terzo libro delle coniche di Apollonio, La Hire dimostrò che il punto di tangenza A della terza retta è il punto di intersezione delle rette ZD e TE, essendo Z e T individuati sui prolungamenti delle tangenti in modo tale che CZ=CE e DB=BT.
Il metodo proiettivo che in quest'opera viene introdotto da La Hire, e che sarà anche il fondamento delle Sectiones conicae, ha la sua ragion d'essere nella divisione armonica di un segmento (vedi qui ).
Nel lemma 1 La Hire dimostrò come trovare il punto B, quarto armonico, quando sono dati i punti A, D e C:
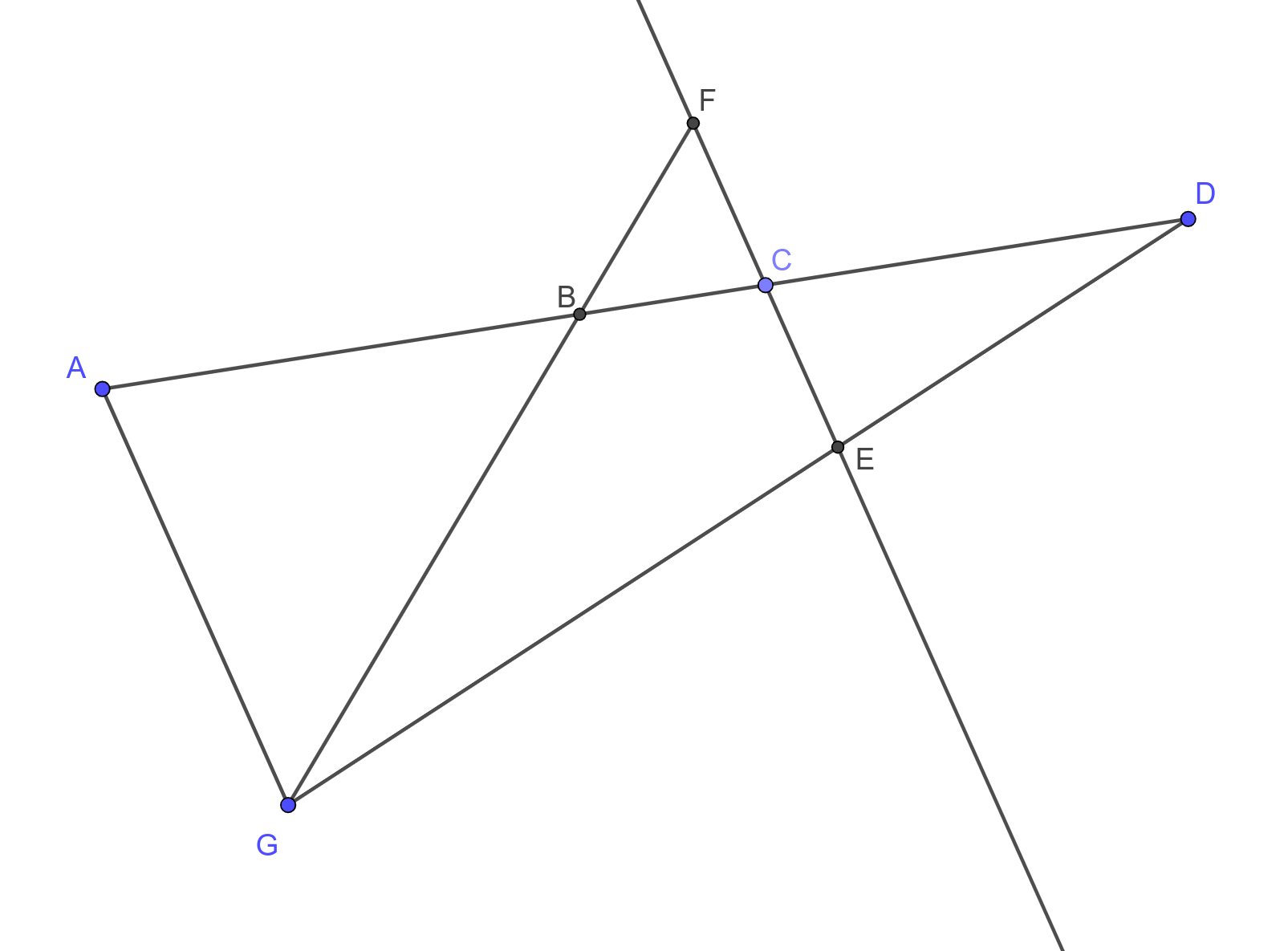
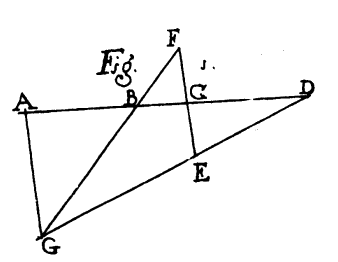
sia dunque dato un segmento AD ed un suo punto interno C. Si prenda un punto qualunque G, non appartenente al segmento, e si tracci il segmento AG (vedi figura 5). Si tracci poi la retta per C parallela al segmento AG, che individua in DG il punto E, e il suo simmetrico F rispetto a C sulla retta CE. L'intersezione del segmento FG su AD individua il quarto armonico B, formando così la quaterna armonica ABCD, tale che \( \frac{BA}{BC}=\frac{DA}{DC}\).
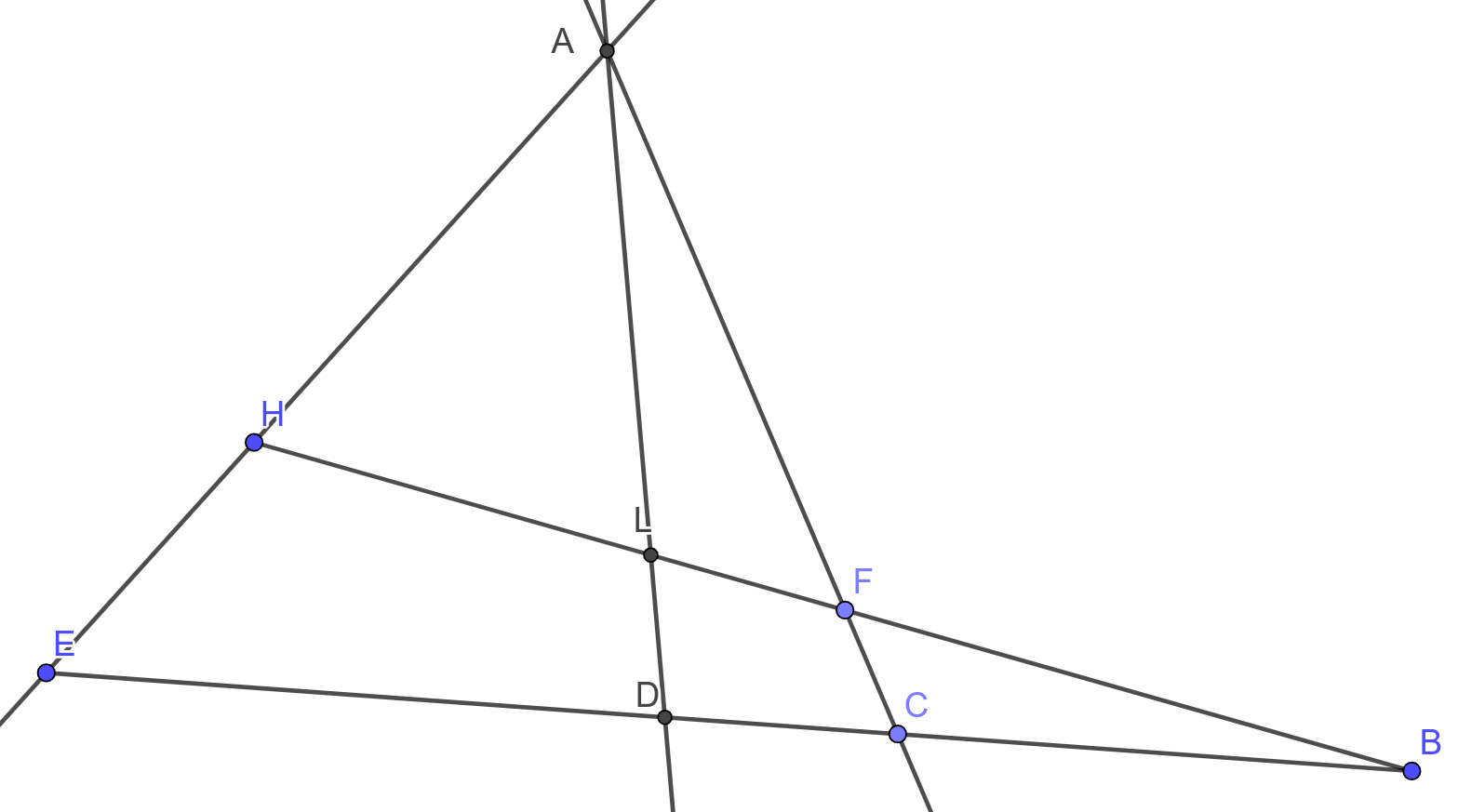
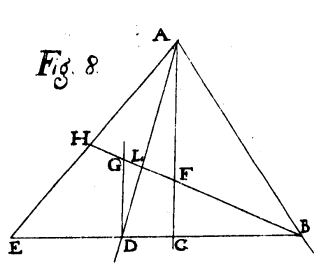
Nei successivi lemmi 2-6 dimostrò l'invarianza proiettiva della divisione armonica, nel caso di rette parallele e nel caso di rette incidenti. La Hire considerò i due casi separatamente perché non concepiva i punti all'infinito. Nel lemma 7 poi dimostrò il viceversa, cioè il fatto che se BE e BH sono divisi armonicamente da D, C e L, F rispettivamente, allora le rette EH, DL e CF si intersecano nello stesso punto A, oppure sono tutte parallele tra loro (figura 6 a destra). Per la dimostrazione procedette per assurdo supponendo che DL non passi per il punto A (retta DG della figura 6 a destra).
La Hire studiò la relazione “polo-polare” (lemmi 10 e 11) rispetto a un cerchio, ma senza l'utilizzo di tale terminologia, che invece sarà usata in questa sede per semplicità.
Per definire la polare di un punto rispetto a un cerchio si distinguono tre casi, a seconda che il punto P sia esterno al cerchio, appartenente al cerchio oppure interno al cerchio.
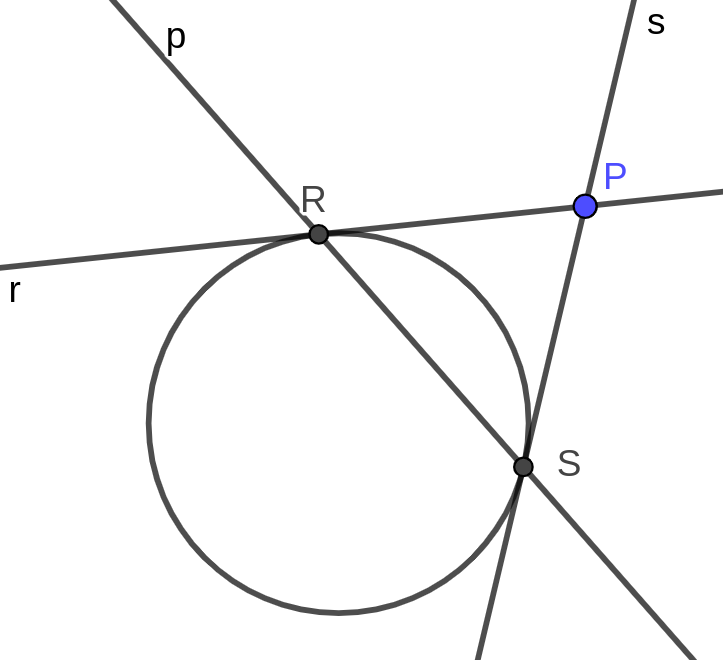
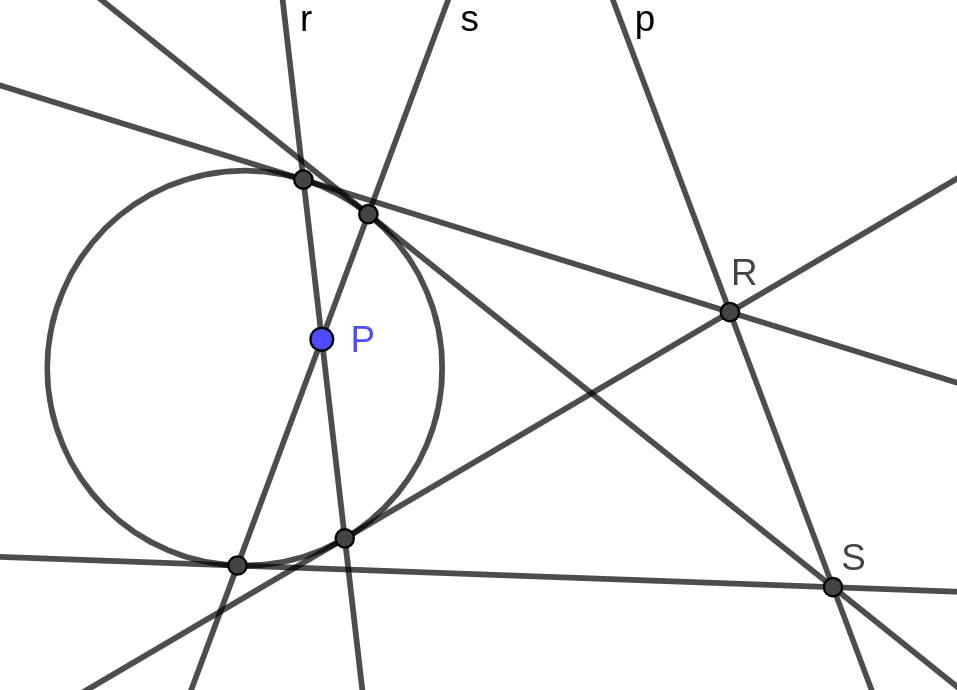
Si prendano in considerazione un cerchio ed un punto P esterno ad esso. Si traccino le rette r ed s tangenti rispettivamente in R ed S al cerchio e passanti per P. Allora la retta polare p del cerchio rispetto a P è la retta RS (figura 7).
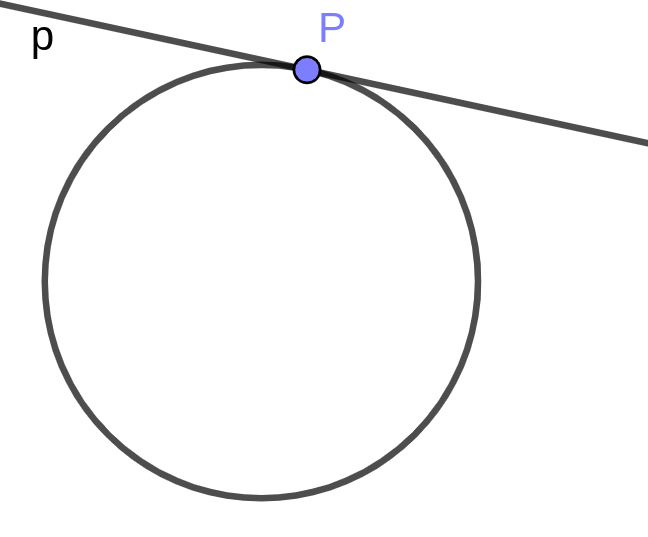
Nel caso il punto P sia appartenente al cerchio, P va visto come la sovrapposizione di R ed S, quindi la polare sarà semplicemente la tangente in P (figura 8).
Se invece il punto P è interno al cerchio, si procede tracciando due secanti qualunque r ed s passanti per P. Si tracciano poi le tangenti al cerchio passanti per i punti in cui le rette r ed s intersecano la curva. Le tangenti per i punti di intersezione con r si intersecano in R, quelle per i punti di intersezione con s in S. La retta RS è la polare di P (figura 9). Si osservi che la retta p non dipende da r ed s: una volta fissato P, qualunque sia la scelta delle secanti, i punti di intersezione delle tangenti nei punti di intersezione R ed S giaceranno sulla polare p.
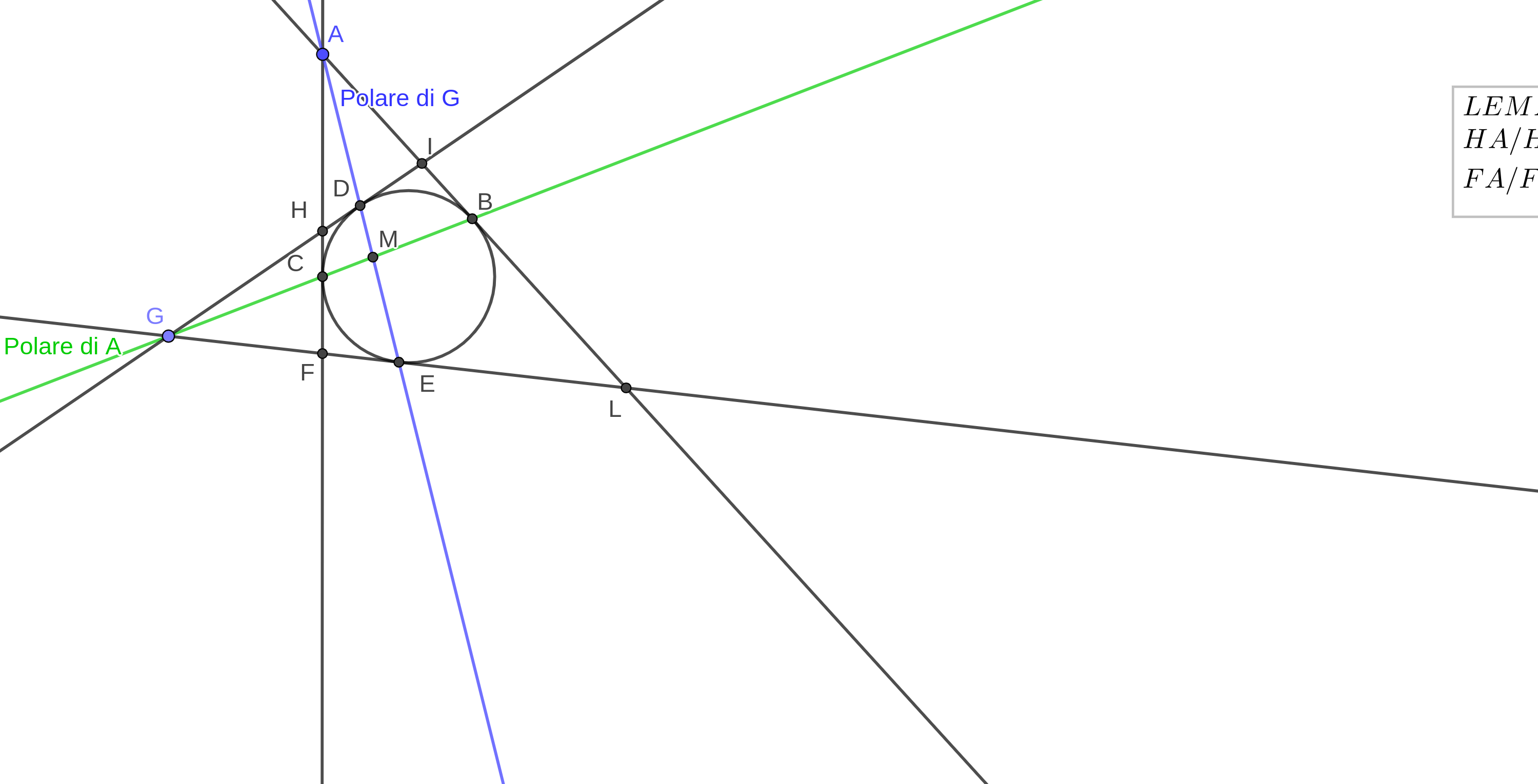
Usando i risultati precedenti, con il lemma 17 dimostrò che se A e G sono due punti esterni al cerchio, uno sulla polare dell'altro, allora ciascuna tangente da A (o da G), è divisa armonicamente dai punti di intersezione con le due tangenti da G (o da A), e il suo punto proprio di contatto (ossia il punto di intersezione della tangente con il cerchio, vedi figura 10). Ad esempio AF x HC=AH x FC.
Più avanti passò quindi allo studio delle sezioni coniche, ma mettendo prima la trattazione di quella che chiamò la formazione di oggetti, e questo per aiutare l'immaginazione come egli stesso scrisse. Tale formazione di oggetti consiste di fatto nella proiezione centrale. Dato un punto x, la sua formazione, in un dato piano, da un punto A non appartenente al piano, è il punto X di intersezione tra la retta Ax e il piano dato. Pertanto la formazione di una retta è una retta, e la formazione di un cerchio è una sezione conica.
La Hire oltre al piano della sezione prese anche in considerazione il piano parallelo a quest'ultimo e passante per il vertice del cono (il polo della formazione), e definì la sezione conica un'ellisse, una parabola o un'iperbole, a seconda che la retta che questo piano taglia sul piano del cerchio sia esterna, tangente o secante al cerchio. Nelle Sectiones conicae La Hire chiamò il piano passante per il vertice piano verticale e la retta direttrice.
L'opera fu pubblicata nel 1674 come supplemento al Nouvelle méthode, e in essa La Hire presentò le trasformazioni piane suggerite nelle costruzioni del Nouvelle méthode, ma in maniera più moderna e diretta. Come scrisse nell'introduzione, intese Les Planiconiques come un'alternativa al Nouvelle méthode, “in quanto molte persone che ne sanno di geometria tuttavia non sono abituate alla rappresentazione piana di figure solide”. Ad ogni modo, non fu solo un aiuto nella comprensione del Nouvelle méthode: per la prima volta nella storia infatti è qui definita una trasformazione che permette lo studio delle proprietà delle sezioni coniche tramite le proprietà del cerchio. Inoltre il suo approccio introdusse, almeno in forma embrionale, il concetto di “trasformazione piana”, anticipando quella di omologia piana.
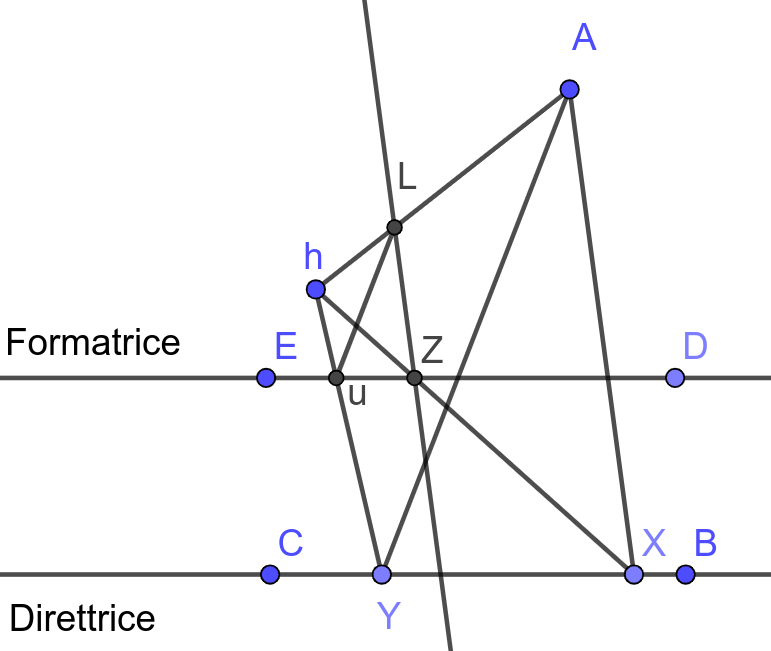
riproduzione della figura 84 delle Planiconiques, 1674
Per definire la sua trasformazione La Hire considerò nel piano due rette parallele BC e DE (figura 11), che chiamò rispettivamente direttrice e formatrice, e un punto A che non sta su BC che chiamò polo. Poi, fissato un punto X su BC, per qualsiasi punto h non facente parte delle due rette e diverso da A, considerò l'intersezione Z delle rette hX e DE. Condusse poi da Z la parallela ad AX, e chiamò L la sua intersezione con la retta Ah. Poiché L non dipende dalla scelta di X, La Hire definì L il formato di h (formé). Tuttavia chiameremo “trasformato” anziché “formato” qualsiasi oggetto ottenuto in maniera simile.
Alla pagina 78 delle Planiconiques La Hire dichiarò: “le sezioni di superfici coniche sono linee curve formate attraverso questo metodo”; ossia, qualunque sezione conica può essere ottenuta come trasformata di un cerchio. Per provarlo, procedette considerando un cono e un piano che lo seziona generando una parabola. Poi trasformò col suo metodo alcuni punti della conica sul piano del cerchio di base del cono, ottenendo punti della circonferenza. Infine, nella parte rimanente delle Planiconiques, dimostrò vari teoremi riguardanti i tre tipi di sezioni coniche: parabola, iperbole ed ellisse. Nel caso della parabola, mostrò che i punti medi di tutti i segmenti paralleli tra loro e aventi le estremità sulla parabola, giacciono su una retta. La Hire chiamò questa retta diametro, e i segmenti paralleli ordinate. Per l'iperbole mostrò invece che gli asintoti sono le trasformate delle tangenti al cerchio di base nei suoi punti di intersezione con la direttrice. Dimostrò inoltre teoremi validi per qualunque sezione conica, come per esempio le proprietà “polo-polare”.

Datata 1685, la pubblicazione è considerata “l'opera magna” di Philippe de La Hire: un trattato in nove libri, di circa 250 pagine e con figure numerate inserite nel testo. In quest'opera La Hire presentò tutte le conoscenze relative alle sezioni coniche dall'antichità fino a quel momento, e per la prima volta nella storia le dimostrò in modo uniforme ed elegante, con tre eccezioni: il problema delle tre e quattro linee, il teorema di involuzione di Desargues e il teorema dell'esagono di Pascal.
Volgiamo ora l'attenzione all'Expositio brevis, che La Hire incluse alla fine del suo trattato sulle sezioni coniche. Come scrisse nella prefazione (La Hire, 1685), pensò che fosse corretto rendere omaggio al lavoro di Apollonio, aggiungendo un sommario dei sette libri (vedi Figura 13) “che sono giunti fino a noi”, e delle proposizioni ivi dimostrate, in modo che potessero essere confrontate con le sue.
Nel citare tutte le proposizioni di Apollonio, e nel confrontarle con le proprie, sembra che La Hire intendesse dimostrare la superiorità dei metodi che adottò nello sviluppo della teoria delle sezioni coniche, e che volesse rimpiazzare il lavoro di Apollonio con il proprio. In conclusione La Hire non scoprì nuovi teoremi, ma piuttosto presentò tutte le proposizioni di Apollonio in modo sistematico, fornendo inoltre dimostrazioni chiare e più semplici.
Comunque, le Sectiones conicae di La Hire migliorarono fortemente l'idea, già diffusa, delle sezioni coniche come immagine proiettiva del cerchio, e della possibilità quindi di ridurre le loro proprietà a quelle del cerchio.
Sebbene l'opera fu ben accolta in Francia e all'estero (ad esempio Newton la citò nei suoi Principia), il trattato di La Hire non rimpiazzò, come da lui sperato, l'opera di Apollonio, che anzi fu riedita nel 1710 da Halley.

