Keplero e le Coniche
Keplero e le Coniche: un contributo dimenticato
Scarica la ricerca completa e dettagliata
 Figura 1: Ritratto di Giovanni Keplero, copia di un originale del 1610 andato perduto, museo benedettino di Kremsmünster.
Figura 1: Ritratto di Giovanni Keplero, copia di un originale del 1610 andato perduto, museo benedettino di Kremsmünster.
Giovanni Keplero, matematico e astronomo tedesco, è ricordato principalmente per aver scoperto le tre leggi del moto planetario che portano il suo nome.
Molte informazioni sulla vita di Keplero si possono apprendere dalla grande quantità di lettere pervenute.
- 1571 - Keplero nasce in Svevia, primogenito di un soldato mercenario e della figlia di un locandierie.
- Si iscrive all'università di Tubinga con l'intenzione di essere ordinato sacerdote. Grazie alle sue abilità matematiche, viene introdotto al nuovo sistema eliocentrico di Copernico. Abbandona i propositi per l'ordinazione in favore di un posto di insegnamento a Graz.
- 1596 - Pubblicazione di Mysterium Cosmographicum, opera di astronomia, Tubinga.
- 1600 - Keplero inizia a lavorare a Praga come assistente matematico di Tycho Brache, uno dei più importanti astronomi del tempo.
- 1601 - Muore Tycho Brahe. Keplero prende il suo posto come Matematico Imperiale.
- 1604 - Pubblicazione di Ad Vitellionem paralipomena quibus astronomie pars optica traditur, opera di ottica, Francoforte.
- 1609 - Pubblicazione di Astronomia Nova, opera di astronomia, Heidelberg.
- 1612 - L'imperatore Rodolfo II d'Asburgo abdica in favore del fratello, poco tollerante nei confronti dei protestanti. Keplero viene scomunicato e si trasferisce a Linz.
- 1619 - Pubblicazione di Harmonices Mundi, opera di astronomia concepita come seguito del Mysterium Cosmographicum, Linz.
- 1626 - Lascia Linz e lavora per Albrecht von Wallenstein, un capo militare impegnato nella Guerra dei Trent’anni (1618-1648), con il compito di fornire consigli basati sull'astrologia.
- 1628 - pubblicazione delle Tabulae Rudolphinae, molto più accurate delle tavole astronomiche usate in precedenza.
- 1630 - muore a Ratisbona.




 Figura 2: frontespizio delle Tabulae Rudolphinae.
Figura 2: frontespizio delle Tabulae Rudolphinae.
Rende omaggio ai grandi astronomi del passato: Ipparco, Tolomeo, Copernico e Tycho Brahe.
Le opere a carattere matematico di Albrecht Dürer(1471-1528) sono una delle possibili fonti di Keplero.
Sebbene Dürer non fornisca dimostrazioni rigorose, suggerisce comunque un metodo pratico per disegnare le coniche.
Dopo aver rappresentato la sezione verticale del cono e il suo cerchio di base, questo metodo prevede di considerare una serie di punti distribuiti a piacere lungo la linea (segmento fg) che rappresenta il piano di taglio, che è il piano della conica, e ripetere per ciascuno il seguente procedimento.
Per ogni punto si tracciano due rette:
- una retta parallela alla linea di terra;
- una retta parallela all’asse del cono.
La retta parallela alla linea di terra intersecherà i lati del triangolo in due punti.
Si considera quindi la circonferenza avente raggio pari alla metà del segmento individuato da questi due punti e come centro il centro del cerchio di base del cono.
La circonferenza così ottenuta intersecherà la retta parallela all’asse del cono in due punti, che rappresentano le proiezioni dei punti della conica sul piano orizzontale.
Per ottenere la rappresentazione della conica nel suo piano, per esempio nel caso dell’ellisse (si veda la figura a destra nella tavola 3 tratta dall’opera di Dürer), con il compasso si riportano, perpendicolarmente alla linea di terra, il segmento fg e i punti presi su di esso. Le due estremità del segmento rappresentano le estremità dell’ellisse nel suo piano. Per ogni punto restante si tracciano la retta perpendicolare al segmento fg, e la circonferenza con centro nel punto considerato e raggio pari alla metà della corda individuata dalla corrispondente coppia di punti nel piano orizzontale, proiezioni dei punti della conica. I punti di intersezione di questa circonferenza con la retta perpendicolare al segmento fg sono i punti della conica.
Il procedimento seguito da Dürer sembra quindi un buon metodo per disegnare le sezioni coniche, e probabilmente il fatto che la rappresentazione dell'ellisse nel suo piano non sia simmetrica
è dovuta alla confusione generata dall'abitudine del tempo di chiamare tale curva "ovale".
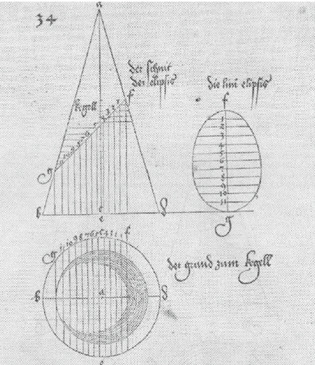 Figura 3: costruzione dell'ellisse nell’opera del Dürer.
Figura 3: costruzione dell'ellisse nell’opera del Dürer.
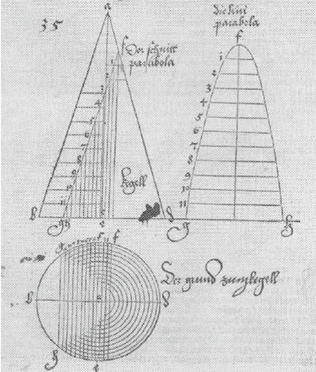 Figura 4: costruzione della parabola nell'opera del Dürer.
Figura 4: costruzione della parabola nell'opera del Dürer.
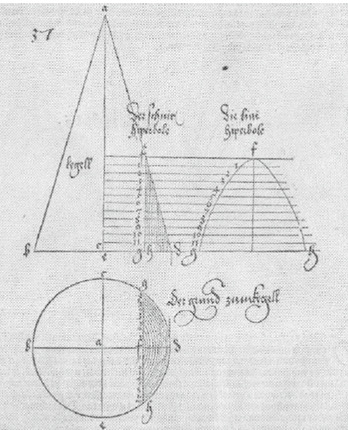 Figura 5: rappresentazione dell'iperbole nell'opera del Dürer.
Figura 5: rappresentazione dell'iperbole nell'opera del Dürer.
Si rendono disponibili le costruzioni delle coniche riprodotte con Geogebra:
L’interesse di Keplero per le coniche ha origine probabilmente dallo studio degli specchi ustori, e le sue considerazioni sull’argomento si trovano
dapprima nell’Astronomiae pars optica, che è essenzialmente un lavoro sull’ottica. Volendo intraprendere uno studio delle coniche indipendente
da quello dei suoi predecessori, con l’obiettivo di fornire una teoria unitaria delle coniche, Keplero elabora il breve trattato De coni sectionibus, inserito nell’Astronomiae pars optica.
Le descrizioni fornite da Keplero suggeriscono che dato un cono Γ, per esempio retto, di vertice V e con base il cerchio C, il sistema di sezioni coniche Λ di cui parla Keplero si ottenga tagliando il cono
con i piani passanti per la retta L che incontra il cono nel punto P e che giace su un piano parallelo al piano di C, non passante per V. Keplero considera Λ un sistema continuo,
nel quale le coniche possono essere trasformate le une nelle altre grazie alla rotazione continua del piano passante per L.
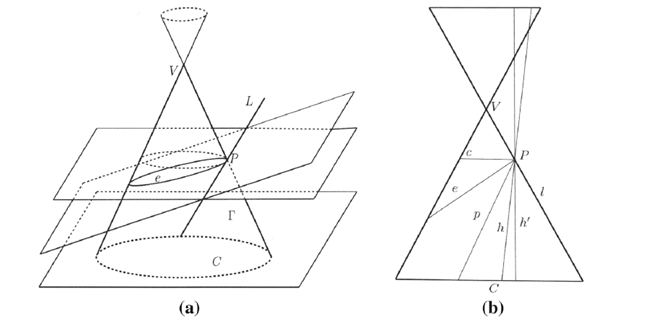 Figura 6: a) il cono Γ e la sua sezione e che giace su un piano passante per la retta L. b) Rappresentazione della sezione del cono per opera di un piano σ passante per il suo asse e ortogonale alla retta L. Le sezioni coniche ottenute dai piani passanti per L sono identificate dalla traccia lasciata da questi piani sul piano σ, e sono indicate con le lettere l, h’ (piano parallelo all’asse del cono), h, p, e, c, che rappresentano rispettivamente: retta, iperbole, iperbole, parabola, ellisse e cerchio.
Figura 6: a) il cono Γ e la sua sezione e che giace su un piano passante per la retta L. b) Rappresentazione della sezione del cono per opera di un piano σ passante per il suo asse e ortogonale alla retta L. Le sezioni coniche ottenute dai piani passanti per L sono identificate dalla traccia lasciata da questi piani sul piano σ, e sono indicate con le lettere l, h’ (piano parallelo all’asse del cono), h, p, e, c, che rappresentano rispettivamente: retta, iperbole, iperbole, parabola, ellisse e cerchio.
Keplero mostra la possibilità di passare in modo continuo da una conica all'altra grazie al principio di analogia, che esprime il principio secondo il quale due figure, apparentemente diverse, sono connesse tra loro in modo continuo attraverso infinite forme intermedie progressivamente simili alle due figure.
Il sistema piano di coniche proposto da Keplero viene introdotto subito dopo la definizione dei fuochi delle coniche, indicati come quei punti F che godono della proprietà che le rette che congiungono tali punti con un punto P qualsiasi della conica,
formano con la tangente alla conica nel punto P angoli uguali.
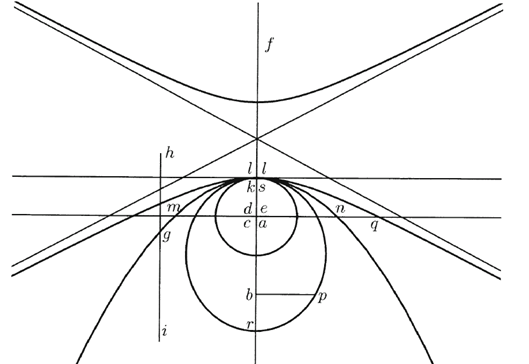 Figura 7: sistema piano di coniche proposto da Keplero.
Figura 7: sistema piano di coniche proposto da Keplero.
Come si vede in figura, Keplero ha concepito un sistema piano di coniche che hanno un vertice in comune nei punti k=l=s, l’asse maggiore fr in comune, un fuoco fisso nei punti a=c=d=e,
e l’altro libero di muoversi lungo fr. Partendo dal cerchio, quando b=a, muovendo b verso il basso lungo l’asse fr si passa attraverso infinite ellissi,
che sono sempre più "acute" man mano che b si allontana da a, fino a quando b si trova a una distanza infinita dal fuoco fisso e la conica è diventata una parabola. Il punto b viene in qusto caso chiamato "fuoco cieco".
Riavvicinando b, ora dalla parte opposta dell’asse e indicato con f, si giunge, passando per la parabola, alle iperboli, che sono sempre più "ottuse" man mano che f si avvicina ad a.
Keplero ha perciò immaginato il suo sistema attraverso il movimento continuo di b lungo l’asse fr, che corrisponde alla rotazione del piano passante per la retta L rappresentato in figura 6a.
Grazie alla descrizione fatta da Keplero, si comprende il significato degli aggettivi “ottusa” e “acuta” quando riferiti a una sezione conica: di tutte le ellissi la più ottusa è il cerchio,
poiché i fuochi coincidono con il centro, mentre la più acuta è la parabola, poiché i fuochi si trovano ad una distanza infinita, e l’iperbole è più ottusa quanto minore è la distanza tra i suoi fuochi.
Quindi, poiché la linea è la più ottusa delle iperboli, nella posizione limite la distanza tra i due fuochi deve essere la minore possibile.
Cliccare qui per la costruzione interattiva del modello proposto da Keplero.
Sebbene non siano stati affermati in modo esplicito, in questo lavoro si trovano due concetti che diventeranno i principi di base della geometria proiettiva:
- Due punti opposti all’estremità di una linea retta possono essere pensati come lo stesso punto;
- Linee parallele si incontrano in un punto all’infinito.
Sfortunatamente le idee di Keplero furono scordate, probabilmente oscurate dai suoi successi in astronomia, e bisognerà attendere Poncelet (1788-1867) prima che vengano riscoperte e sviluppate nel suo trattato sulle proprietà prospettiche delle figure.











